Übungen und Tabellenblätter ↓ ⇓
- Einfache Formeln eingeben
Währungsrechner - Formatierungen
Zahlenformate bergen besonders für Anfänger Überraschungen.
Alter in Tagen berechnen, Zeiterfassung sind Übungen mit Zeit und Datum. (Musterlösung mit Kurzanleitung)
- Externe Variable leicht zugänglich in eigene Zellen schreiben und per absoluter Adressierung in Formeln einbinden
Artikelliste rechnet Bruttopreise aus Nettopreis und Mehrwertsteuer. (Anleitung auf dieser Seite und Musterlösung)
Preisliste rechnet Währungen mit dem Wechselkurs um. (Musterlösung mit Kurzanleitung)
- Würfelsumme, Großes 1x1: Übungen zum Kopieren mit relativen und absoluten Bezügen. (Musterlösung mit Kurzanleitung)
- Kernstück meines Kurses, das die Stärken einer Tabellenkalkulation zeigt
Der Tilgungsplan berechnet Zins und Zinseszins mit sehr einfachen Formeln, die geschickt kopiert werden. (Musterlösung und Arbeitsblatt mit Anleitung)
Die Sammelbestellung berechnet die Gesamtpreise aus Bestellmengen und Einzelpreisen und ermittelt den Wechselgeldbedarf mit Stückelung. Der letzte Teil knüpft an den Tilgungsplan an, ist aber deutlich komplizierter. (Musterlösung und Arbeitsblatt mit Anleitung)
- Eingabe von Formeln mit dem Funktionsassistenten
Die Wahrscheinlichkeit für 6 Richtige im Lotto mit der hypergeometrischen Funktion ermitteln. (Anleitung auf dieser Seite) - Tabellenblätter zur praktischen Verwendung (Musterlösungen und Arbeitsblätter mit Anleitungen):
Hypergeometrische Verteilung | Binomiale Verteilung | Operationscharakteristiken von AQL-Anweisungen |
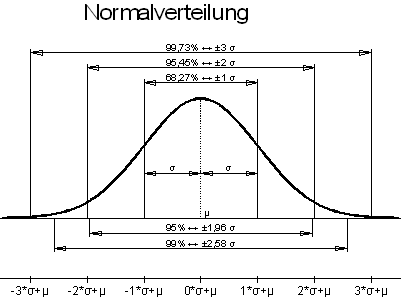
Normalverteilung enthält die Klassierung einer Urwertliste - Diagramme erstellen
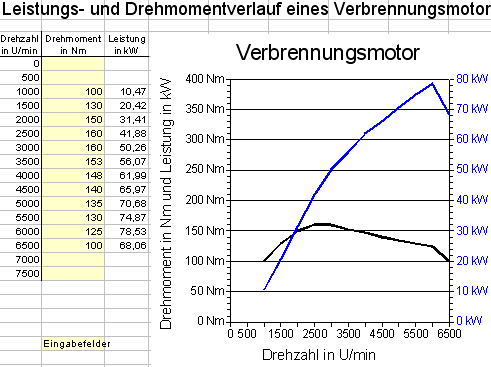
Leistungs- und Drehmomentverlaufskurve enthält 2 Kurven mit zwei verschiedenen y-Achsen. (Anleitung auf dieser Seite und Musterlösung mit Kurzanleitung)
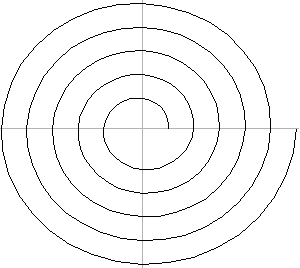
Spirale zeichnen (Musterlösung mit Kurzanleitung)
Phasendiagramme von Zweistofflegierungen als Beispiel für beliebige Liniendiagramme mit Beschriftung. (Anleitung auf dieser Seite)
Geschwindigkeits-Zeit-Diagramm für den senkrechten Wurf als y- und als xy-Diagramm mit Lösungshinweisen - Musterlösungen für Diagramme ohne weitere Hinweise
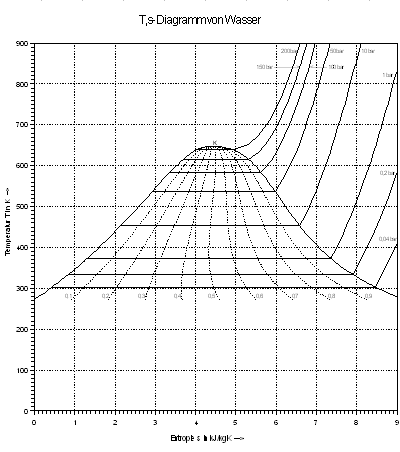
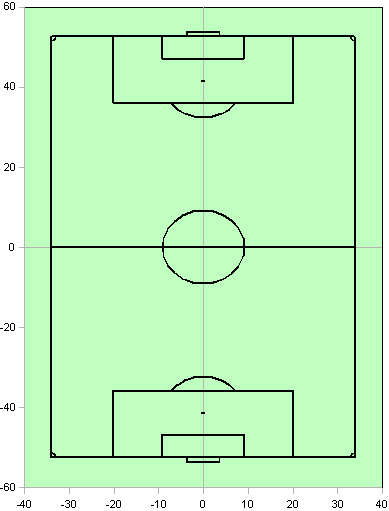
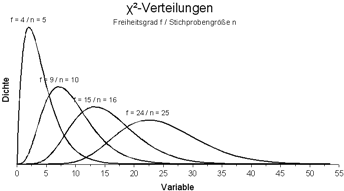
Beispiele für y-Diagramme | Diagramm einer Normalverteilung mit Beschriftung | T, s-Diagramm von Wasser | χ²-Verteilung (Chi²-Verteilung; Chi-Quadrat-Verteilung) | Fußballfeld | Spannungs-Dehnungs-Diagramme - Daten aus einer Tabelle herausziehen
Mit einem Listenfeld zum Aufklappen kann man einen Datensatz aus einer Tabelle manuell auswählen. (Anleitung auf dieser Seite und Musterlösung)
Matrixfunktionen ermöglichen, automatisch den Ort zu einer Postleitzahl oder die Steigung für eine Gewindegröße aus einer Tabelle herauszuziehen. (Musterlösung mit Anleitung)
Datenbankfunktionen erlauben noch komplexere Auszüge, z.B. den Verkäufer mit einem Umsatz und einem Lebensalter von.. bis… (Musterlösung und Kurzanleitung in einem Arbeitsblatt) - Weitere Tabellenblätter
Kalender: Musterlösung und Arbeitsblatt mit Anleitung
Versteckte Spiele in Tabellenkalkulationen: Anleitung
Turnierplan mit Tabelle: Musterlösung
⇑ ↑ 1 Einleitung ↓ ⇓
LibreOffice und OpenOffice sind Zweige desselben Stammes StarOffice, das einst wirtschaftlich an Microsoft scheiterte. 1999 übernahm Sun die Hamburger Firma, gab den Quellcode frei und entwickelte ihn mit der Community als OpenOffice weiter. Nachdem Sun von Oracle übernommen wurde (und inzwischen von der Apache Software Foundation entwickelt wird), trennte sich 2010 ein Teil der Community von OO, um eine alternative Entwicklung unter dem Namen LibreOffice fortzusetzen.
Danach hatte mal die eine, mal die andere Version die Nase vorne, aber momentan (2016) scheinen Apache OpenOffice die freiwilligen Programmierer auszugehen und LibreOffice das Rennen zu machen.
Mit dem hier vorliegenden Kurs möchte ich meinen Schülern die Arbeit mit Tabellenkalkulationen beibringen. Die Unterlagen folgen dem Verlauf meines Unterrichtes, dazu gehören Übungen mit detaillierten Lösungen.
Ich habe den Kurs mit OpenOffice vorbereitet und führe ihn in gemischten Kursen mit OpenOffice und MS Excel durch. Beide Progamme sind also zum Nacharbeiten und Üben geeignet. Mit LibreOffice klappen die meisten Übungen auch, aber in der Praxis muss ich viele meiner alten Tabellen in OpenOffice öffnen, weil sie mit neueren Versionen von LibreOffice nicht mehr funktionieren (siehe Kasten).
LibreOffice / OpenOffice sind sich sehr ähnlich und können kostenlos bei LibreOffice / OpenOffice.de herunter geladen werden. Wegen ihrer Mächtigkeit, Unabhängigkeit vom Betriebssystem und günstigen Preises sind sie meine persönlichen Favoriten. Ich verwende in der Regel neueste Versionen (bei Open Office - siehe rechts), denn sie kosten nichts und im Detail gibt es immer wieder Fortschritte.
MS Excel ist die Tabellenkalkulation innerhalb des MS-Office-Paketes von Microsoft und hat den Vorteil des hohen Verbreitungsgrades. Es läuft nur unter Windows und kostet viel.
⇑ ↑ 2 Allgemeines ↓ ⇓
⇑ ↑ 2.1 Tabelle laden ↓ ⇓
| Übersicht über die Funktionen | OpenOffice / StarOffice | MS Excel |
|---|---|---|
| eine neue Tabelle laden | Datei - Neu - Tabellendokument | Datei - Neu |
| bestehende Tabelle laden | Datei - Öffnen.. | |
Vor der Arbeit muss man erst das Programm und dann eine leere Tabelle aufrufen.
StarOffice und OpenOffice benötigen mehrere Angaben, da sie auch Textdokumente, Präsentationen usw. unter einer Oberfläche bearbeiten können, während Microsoft für jede Aufgabe ein getrenntes Programm bereitstellt.
⇑ ↑ 2.2 Aufbau des Bildschirmes ↓ ⇓
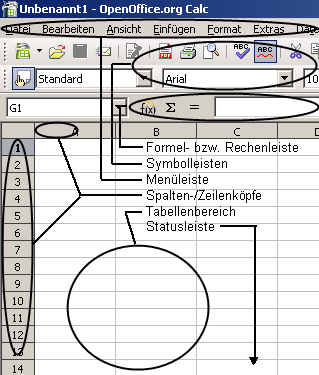
Das Erscheinungsbild von OpenCalc,
der Tabellenkalkulation von OpenOffice 2.0
OpenOffice, StarOffice und MS-Office haben einen ähnlichen Aufbau, der für Windows typisch ist und mittlerweile auch in Linux Einzug gefunden hat.
Die Menüleiste (ganz oben) gibt nach dem Anklicken der Worte weitere Untermenüs frei. Meist findet man im Menü alle Befehle eines Programmes, aber neuere Programme lagern etliche Befehle in die Kontextmenüs aus, die man mit einem rechten Mausklick aufrufen kann.
Die Symbolleisten liegen unter dem Menü und enthalten häufig verwendete Befehle als Bildchen (Icon). Die Befehle werden mit einem Mausklick auf das Icon aufgerufen. Wenn man mit dem Mauszeiger kurz über dem Icon verweilt, wird das Icon erklärt. Symbolleisten können ein- und ausgeblendet und nach eigenen Wünschen gestaltet werden (→ Symbolleisten bearbeiten ).
Die Rechenleiste oder Funktionsleiste dient der Eingabe von Formeln (→ Eingabe von Formeln ).
Die Statusleiste befindet sich meist unterhalb des Tabellenfeldes und gibt Auskunft über aktuelle Einstellungen.
Die Zeilen - und Spaltenköpfe dienen der Adressierung der Zellen. Sie können am Bildschirm oder für den Ausdruck ein- oder ausgeblendet werden (→ Symbolleisten bearbeiten ).
⇑ ↑ 2.3 Symbolleisten und Ansichten bearbeiten ↓ ⇓
| Übersicht über die Funktionen | OpenOffice / StarOffice | MS Excel |
|---|---|---|
| Symbolleisten ein-/ausschalten | Ansicht - Symbolleisten | |
| Leiste für die Formeleingabe ein-/ausschalten | Ansicht - Symbolleisten - Rechenleiste | Ansicht - Bearbeitungsleiste |
| Statusleiste ein-/ausschalten | Ansicht - Statusleisten | |
| Icons einfügen | Ansicht - Symbolleisten - Bearbeiten | Ansicht - Symbolleisten - Anpassen |
| Icons entfernen | Icon auf die Masken Symbolleiste bearbeiten / anpassen ziehen. | |
| weitere Anpassungen | Extras - Anpassen… | |
| Zeilen- und Spaltenköpfe am Bildschirm ausblenden | Extras - Optionen - Tabellendokument - Layout - Zeilen- und Spaltenköpfe | Extras - Optionen - Ansicht - Zeilen- und Spaltenköpfe |
| Zeilen- und Spaltenköpfe für den Ausdruck einblenden | Format - Seite - Tabelle - Zeilen- & Spaltenköpfe drucken | Datei - Seite einrichten - Tabelle - Zeilen- und Spaltenköpfe drucken |
VieleElemente des Bildschirmes können frei gestaltet werden. Dies ist für den Anfänger meistens erst dann nötig, wenn versehentlich eine Leiste verschwunden ist: -)
⇑ ↑ 2.4 Shortcuts und Kontextmenü ↓ ⇓
Neben dem Menü und den Symbolleisten gibt es weitere Eingabehilfen, die die Arbeit mit Programmen erleichtern können.
Shortcuts sind Tastenkombinationen, mit denen man Befehle sehr schnell aufrufen kann. Die Arbeit mit Shortcuts ist dann sinnvoll, wenn man sehr oft mit einem Programm arbeitet, oder wenn es sich um Shortcuts handelt, die in fast jedem Programm gleich sind (z.B. [Strg]+V für Einfügen ).
Man findet die Shortcuts meist in den Menüs.
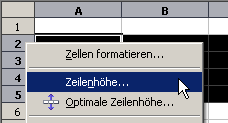
Zeilenhöhe per
Kontextmenu einstellen
Kontextmenüs erscheinen nach einem Klick der rechten Maustaste (RMK). Kontext(-sensitiv) heißt, dass der Inhalt dieser Menüs davon abhängt, an welcher Stelle des Bildschirmes die rechte Maustaste gedrückt wurde und manchmal sogar, welche Tasten zusätzlich gedrückt wurden. Viele Programme setzen stark auf Kontextmenüs (z.B. OpenOffice). Gewöhnen Sie sich an, regelmäßig die rechte Maustaste zu drücken, um zu sehen, welche Befehle angeboten werden.
⇑ ↑ 2.5 Tabelle ↓ ⇓
| Übersicht über die Funktionen | OpenOffice / StarOffice | MS Excel |
|---|---|---|
Tabellenblätter umbenennen | Rechter Mausklick auf Tabellenname | Rechter Mausklick oder Doppelklick auf Tabellenname |
| weitere Aktionen mit Tabellenblättern | Bearbeiten - Tabelle löschen / verschieben / kopieren | Bearbeiten - Blatt löschen / verschieben / kopieren |
Der Tabellenbereich ist das Kernstück jeder Tabellenkalkulation und besteht aus Zellen, die in Zeilen und Spalten angeordnet sind. Jede Zelle hat eine eindeutige Adresse wie beim Spiel "Schiffe versenken", z.B. C13.
In jeder Datei stehen mehrere Tabellenblätter zur Verfügung. Die Tabellenblätter ermöglichen eine übersichtliche Anordnung von mehreren Aufgaben in einem Dokument. Sie können umbenannt, kopiert und verschoben werden, auch in andere Tabellen, wenn diese gleichzeitig geöffnet sind.
⇑ ↑ 3 Zelleninhalte ↓ ⇓
Jede Zelle kann Texte, Zahlen oder Formeln enthalten. Da Zahlen, Text und Formeln unterschiedlich behandelt werden, muss man wissen, woran sie vom Programm erkannt werden.
⇑ ↑ 3.1 Zahlen ↓ ⇓
Zahlen enthalten nur Ziffern und eventuell ein Komma und ein Vorzeichen. Ein Punkt statt des Kommas ist in den deutschen Versionen nicht zulässig.
Achtung: Manchmal sieht eine Zahl kann anders aus, als man es erwartet hat. Wenn von einer Telefonvorwahl die führende Null abgeschnitten wird, ist die Nummer wenigstens noch zu erahnen. Aber was tun, wenn unversehens ein Datum oder eine andere seltsame Zeichenfolge erscheint?
Die Darstellung einer Zahl hängt von ihrer Formatierung ab. Das Problem mit der Telefonvorwahl können lösen, indem Sie sie als Text formatieren. (→ Zahlenformate )
⇑ ↑ 3.2 Funktionen bzw. Formeln ↓ ⇓
| Beispiele für Funktionen | Anzeige bzw. Ergebnis |
|---|---|
| = 1 + 4 | 5 (Zahl) |
| = Summe (C4.. C6) | Summe der Zellinhalte von C4, C5 und C6 (Zahl) |
| = "Name"&", "&"Vorname" | Name, Vorname (Text) |
Mit Funktionen werden Verknüpfungen zwischen Zahlen, Texten oder Zellinhalten (Zahlen oder Texten) durchgeführt. Funktionen beginnen immer mit einem Gleichheitszeichen. Zellinhalte werden über ihre Zelladresse angesprochen und dienen so als Variable.
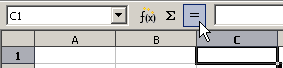
Formel in C1 mit einem
Gleichheitszeichen beginnen
Um eine Funktion einzugeben, markiert man die Zelle und beginnt immer mit einem Gleichheitszeichen. Das Gleichheitszeichen tippt man ein oder wählt es mit der Maus aus der Rechen- bzw. Funktionsleiste. (→ Arbeiten mit Funktionen )
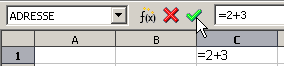
Formel in der Zelle oder in der
Rechenleiste eintippen und abschließen
Nach dem Eingeben des Gleichheitszeichens wird die Rechen- bzw. Funktionsleiste aktiv, und man kann die Formel eintippen oder den Formelassistenten aufrufen.
Um die Formel abzuschließen drückt man die Return -Taste oder klickt auf das grüne Häkchen.
Um die Formeleingabe folgenlos abzubrechen, drückt man die Esc -Taste oder klickt auf das rote Kreuzchen.
Tipp : Wenn Sie die Formeleingabe durch Klick in eine andere Zelle beenden, führt das manchmal zum Erfolg und manchmal zu seltsamen Überraschungen. Deshalb würde ich mir diese Methode gar nicht erst angewöhnen.
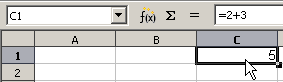
Formel in der Rechenleiste
und Ergebnis der Formel in C1
Nachdem die Bearbeitung der Funktion abgeschlossen ist, wird in der Zelle das Ergebnis der Funktion angezeigt. Die Funktion selbst erscheint in der Rechen- bzw. Funktionsleiste, wenn die Zelle markiert ist. (→ Eingabe von Formeln .)
Tipp : Sollte Sie die Anzeige in der Zelle überraschen, versuchen Sie es einmal in den Kapiteln Fehlermeldungen in Zellen oder Zahlenformate
⇑ ↑ 3.3 Text bzw. Zeichenketten ↓ ⇓
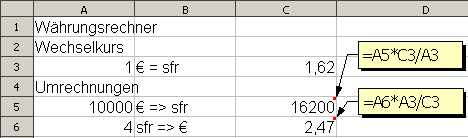
Übung Währungsrechner erstellen
Texte sind das, was übrig bleibt. Es handelt sich um Zeichenketten (Strings), die weder als Zahlen noch als Funktionen erkannt wurden.
Will man Zahlen als Text eingeben, stellt man ein Hochkomma voran (z.B. die Vorwahl '07621). Das ist sinnvoll, weil bei Zahlen die führenden Nullen wegfallen. Das Hochkomma gehört nicht zum Text und wird weder angezeigt noch in Funktionen verarbeitet.
In Funktionen kennzeichnet man Text, indem man ihn in Anführungszeichen setzt (→ Funktionen ). Sie können mit dem kaufmännischen Und "&" (amerikanisch: Ampersand) verknüpft werden.
Übung " Währungsrechner"
Erstellen Sie ein Tabellenblatt zur Umrechnung von Schweizer Franken in Euro nach Muster, vorläufig ohne Formatierung:
Aufgabenbeschreibung mit Lösung: PDF, OpenOffice2, Excel97 .
⇑ ↑ 4 Zellenformate ↓ ⇓
Formatieren bedeutet, die Erscheinungsform einer Zelle oder des Zellinhaltes zu verändern. Dazu gehören
- Zellengröße (Höhe und Breite)
- Zusammenfassen von Zellen
- Formate der Zelle (Äußerlichkeiten wie Hintergrund, Rahmen, Schriftart und -größe usw.)
- Schriftformate (Größe, Schriftart, Richtung, Ausrichtung)
- Zahlenformate (Datum, Prozent usw.)
- Schutzfunktionen gegen Veränderungen von Zellen
Tipp : Formate können auch vom Zellinhalt abhängig gemacht werden (→ bedingte Formate ). Mit bedingten Formaten kann eine Zelle automatisch einen roten Hintergrund erhalten, wenn ein Termin fällig oder ein Konto überzogen ist.
Tipp : es gehört zu einem guten Programmierstil, Inhalt und Form einer Zelle zu trennen. Dazu ist eine weiche Formatierung geeignet. (→ Formatvorlagen )
Unterrichtshinweis: Ich gehe auf die äußerlichen Formate der Zelle im Unterricht nur ganz kurz ein, weil die Schüler dies im Rahmen des Spieltriebes meist schnell selbst lernen, wenn auch nur die unprofessionelle harte Formatierung.
⇑ ↑ 4.1 Zellen aktivieren ↓ ⇓
Bevor Zellen formatiert oder sonstwie bearbeitet werden können, müssen sie aktiviert werden.
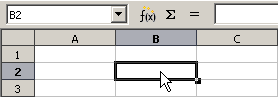
Aktivieren der Zelle B2
Einzelne Zellen aktiviert man durch einen Klick in die Zelle.
Die Adresse der Zelle wird im Adressfeld angezeigt, außerdem werden die Spalten- und Zeilenköpfe der Zellen hervorgehoben.
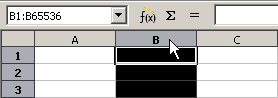
Aktivieren der Spalte B
Ganze Spalten oder ganze Zeilen aktiviert man, indem man mit gedrückter linker Maustaste über die Spalten- oder Zeilenköpfe fährt.
Der Adressbereich der Zellen wird im Adressfeld angezeigt, außerdem werden die Spalten- oder Zeilenköpfe der Zellen hervorgehoben.
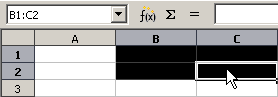
Aktivieren des Zellbereiches B1: C2
Rechteckig zusammenhängende Zellbereiche aktiviert man, indem man mit gedrückter linker Maustaste über den Zellbereich fährt.
Beachten Sie im Adressfeld, wie rechteckig zusammenhängende Zellbereiche adressiert werden, hier lautet die Adresse B1: C2 Außerdem werden die Spalten- und Zeilenköpfe der Zellen hervorgehoben.
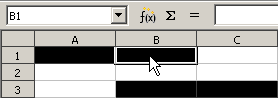
Aktivieren von
nicht zusammenhängenden
Zellen A1: B1 B3: C3
Nicht zusammenhängende Zellen aktiviert man, indem man beim Anklicken der zweiten und der weiteren Zellen die Strg-Taste gedrückt hält.
Im Adressfeld wird nur die Adresse der jeweils zuletzt aktivierten Zelle angezeigt, Spalten- und Zeilenköpfe werden nicht hervorgehoben.
| Übersicht über die Funktionen | OpenOffice / StarOffice | MS Excel |
|---|---|---|
| Zelle markieren | Zelle Anklicken | |
| ganze Spalten / Zeilen markieren | Spalten- / Zeilenkopf anklicken | |
| rechteckige Bereiche markieren | Eine Zelle anklicken und dann über die anderen Zellen fahren, ohne die Maustaste loszulassen | |
| mehrere Bereiche markieren | Den 1. Bereich markieren, bei den folgenden Bereichen die [Strg] - Taste gedrückt halten. Bei älteren StarCalc-Versionen funktioniert dies nur, wenn der 1. Bereich mehr als eine Zelle umfasst. | |
⇑ ↑ 4.2 Zellengröße, Zeilen und Spalten ↓ ⇓
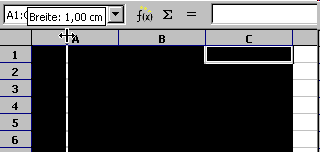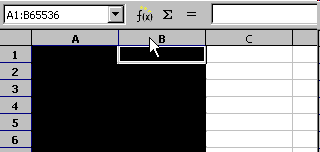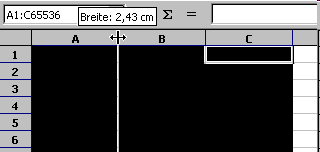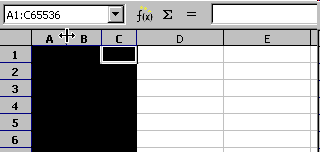
Animation: Breite mehrerer Spalten
einheitlich mit der Maus einstellen
Die Breite der Spalten und die Höhe der Zellen können festgelegt werden, indem man die Grenzen zwischen den Spalten- bzw. Zeilenköpfen verschiebt.
- Aktivieren Sie eine oder mehrere Spalten, indem Sie mit gedrückter linker Maustaste über die Spaltenköpfe fahren.
- Packen Sie dann die Grenze zwischen 2 Spalten, indem Sie die linke Maustaste drücken. Achten Sie darauf, dass der Mauszeiger die Form eines Kreuzes annimmt.
- Verschieben Sie die Grenze, und verändern Sie so die Breite einer Spalte. Wenn Sie die Maus loslassen, übernehmen die anderen aktivierten Spalten die eingestellte Breite.
Mit der Zeilenhöhe funktioniert es genauso.

Zeilenhöhe per Kontextmenu einstellen
Die Breite der Spalten und die Höhe der Zellen kann auch in den Menus festgelegt werden.
- Aktivieren Sie eine oder mehrere Zeilen, indem Sie mit gedrückter linker Maustaste über die Zeilenköpfe fahren.
- Drücken Sie dann die rechte Maustaste, solange sich der Mauszeiger noch über den Zeilenköpfen befindet.
- Wählen Sie "Zeilenhöhe", um die Zeilenhöhe im cm angeben wollen, oder "optimale Zeilenhöhe", wenn sich die Zeilen automatisch an die Schrift anpassen sollen.
Mit der Spaltenbreite funktioniert es natürlich genauso.
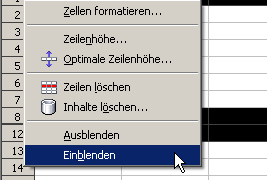
Ausgeblendete Zeilen wieder einblenden
Mit dem gleichen Kontextmenu kann man Zeilen auch löschen, hinzufügen und aus- und einblenden.
Nach dem Ausblenden sind die Zeilen zwar noch vorhanden, werden aber nicht mehr angezeigt. Man erkennt es an der nicht fortlaufenden Nummerierung der Zeilen (siehe Bild, die Zeilen 9.. 11 sind ausgeblendet, die Zeilen acht.. 12 sind aktiviert).
Ausblenden ist sinnvoll, wenn man Nebenrechnungen verstecken will.
Ausgeblendete Bereiche werden wieder sichtbar gemacht, indem man die Zeilen darüber und darunter markiert und "Einblenden" im Kontextmenu wählt. (siehe Bild).
Mit der Spalten funktioniert es das natürlich auch.
| Übersicht über die Funktionen | OpenOffice / StarOffice | MS Excel |
|---|---|---|
| Spaltenbreite / Zellenhöhe verändern | Spalten bzw. Zeilen markieren Format - Spalten / Zeilen oder Kontextmenü | |
Hinweis: Zellen einer Spalte haben immer dieselbe Breite und liegen genau übereinander, bei Zeilen ist es ähnlich.
Wenn man Formulare mit Feldern erstellen möchte, die scheinbar keinen Zusammenhang zueinander haben, muss man ein kleines Spaltenraster wählen und Zellen zusammenfassen (→ Formulare ).
⇑ ↑ 4.3 Zellen zusammenfassen ↓ ⇓
verbundene Zellen
Mehrere Zellen können zusammengefasst werden. So kann eine zentrierte Überschrift über mehreren Spalten erreichen oder Formulare aufbauen, bei denen die Matrix des Tabellenblattes nicht erkennbar ist. Die zusammengefassten Zellen müssen in einem rechteckigen Bereich liegen, sie erhalten die Adresse der Zelle oben links.
| Übersicht über die Funktionen | OpenOffice / StarOffice | MS Excel |
|---|---|---|
| Zellen zusammen | Format - Zellen verbinden | Format - Zellen - Ausrichtung - Zellen verbinden |
Hinweis: Zusammengefasste Zellen machen immer wieder Schwierigkeiten, wenn das Tabellenblatt bearbeitet wird. Zellen sollte man deshalb so spät wie möglich zusammenfassen.
Hinweis II: Zusammengefasste Zellen sind eine Möglichkeit, Formulare zu erstellen, deren untereinander liegenden Formularfelder nicht dieselbe Größe haben sollen (→ Formulare ).
⇑ ↑ 4.4 Formate der Zelle ↓ ⇓

Formate der Zellen
Für jede Zelle können Hintergrundfarben, Rahmen, Rahmenfarben usw. festgelegt werden.
| Übersicht über die Funktionen | OpenOffice / StarOffice | MS Excel |
|---|---|---|
| Zellen formatieren | Format - Zelle - Umrandung Format - Zelle - Hintergrund | |
⇑ ↑ 4.5 Schriftformate ↓ ⇓

Verschieden formatierte Schriften
Schriften können auf verschiedene Arten formatiert werden. Die Möglichkeiten sind zwar nicht so umfangreich wie in einer Textverarbeitung, aber immerhin kann man inzwischen innerhalb einer Zelle mehrere Schriftformate verwenden, und zB. lateinische und griechische Buchstaben mischen.
Die tiefer gestellten Indexe im Bild sind mit verschiedenen Schriftgrößen vorgetäuscht.
| Übersicht über die Funktionen | OpenOffice / StarOffice | MS Excel |
|---|---|---|
| Schrift | Format - Zellen - Schrift Format - Zellen - Schrifteffekt Format - Zellen - Ausrichtung | |

Übung Währungsrechner formatieren
Tipp: es ist immer eine gute Idee, ein Blatt erst dann äußerlich in Form(at) zu bringen, wenn alles funktioniert und ausgetestet ist. Ein Blatt zwischendurch schön zu machen, um die Formatierung bei der nächsten Änderung wieder zu löschen, kostet einfach nur unnötige Zeit.
Tipp II: Markieren Sie ihre Blätter so, dass Sie auch in 2 Jahren noch auf Anhieb wissen, wo Sie etwas eingeben können oder müssen.
Tipp III: Wenn Sie ganz sicher gehen wollen, dass mühsam erstellte Formeln nicht versehentlich überschrieben werden können, müssen Sie die betreffenden Zellen schützen (→ Zellschutz ).
Übung " Währungsrechner "
Formatieren Sie den Währungsrechner nach der Musterlösung.
Die Musterlösungen PDF, OpenOffice2, Excel97 sind dieselben wie oben.
⇑ ↑ 4.6 Zahlenformate ↓ ⇓
4.6.1 Zahlenformate zuweisen
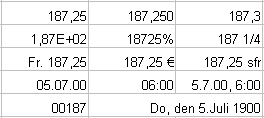
Die Zahl 187,25 in verschiedenen Formaten
Zahlenformate verändern die äußere Darstellung einer Zahl, aber nicht ihren Wert. Intern bleiben die Zahlen unverändert, d.h. eine Tabellenkalkulation rechnet immer mit allen vorhandenen Kommastellen, auch wenn sie nicht sichtbar sind.
Das Aussehen der Zahl ändert sich manchmal so drastisch, dass die Zahl nicht wiederzuerkennen ist. Für Anfänger ist dies eine häufige Quelle von Überraschungen. Sollte Ihnen eine solche Überraschung widerfahren, entfernen Sie das Zahlenformat (s.u.) oder suchen Sie die Ursache bei den Fehlermeldungen .
Aktivieren Sie die Zellen, und wählen Sie das Format:
Übung " Zahlenformate "
Formatieren Sie die Zahl 187,25 wie im Bild dargestellt.
Lösungshinweise mit Musterlösung: PDF, LibreOffice, Excel97 .
| Übersicht über die Funktionen | OpenOffice / StarOffice | MS Excel |
|---|---|---|
| Zahlenformat zuweisen | Format - Zelle - Zahlen | |
| Zahlenformat entfernen | Format - Zelle - Zahlen - Alle - Standard | Format - Zellen - Zahlen - Löschen |
4.6.2 Automatische Zahlenformatierungen
Manche Formatierungen werden automatisch erzeugt, wenn die Zahl geeignet (oder ungeeignet, wenn es dumm läuft) eingegeben wird. Dies betrifft vor allem Datum, Zeit und Prozent. Vor der Eingabe muss man die betroffenen Zellen aktvieren .
| Eingabe | Darstellung | Format |
|---|---|---|
| 30-4-2001 30-4-01 | 30.04.01 | Datum (intern 37011) |
| 16:0 | 16:00 | Zeit (intern 0,6666667) |
| 15% | 15% | Prozent (intern 0,15) |
Wenn man eine Zahl normal eingibt, und sie trotzdem als Datum oder Uhrzeit dargestellt wird, kann es zwei Ursachen geben.
- Die Zelle war vorher schon als Datum (Uhrzeit) formatiert, z.B. weil dort früher mal ein Datum stand.
- Der Zellinhalt wird aus einem Datum (Uhrzeit) berechnet.
In beiden Fällen können Sie die Formatierung entfernen, wie es im obigen Kapitel beschrieben ist.
4.6.3 Datum und Zeit
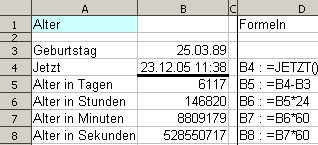
Nee, das ist nicht mein Geburtstag
Tabellenkalkulationen speichern ein Datum nicht mit Tag, Monat und Jahr, sondern zählen die Anzahl der Tage ab dem 01.01.1900. Vor dem Komma werden die Tage gezählt, nach dem Komma auch - und zwar als Bruchteile eines Tages, dort sind also die Stunden versteckt.
Deshalb ist 187,25 als Datum der 05.07.1900 um 6:00 Uhr früh
Die Uhrzeit errechnet man aus 0,25 mal 24 Stunden. Wenn man mit Stunden weiter rechnen möchte, z.B. um ein Gehalt zu berechnen, muss man sie unter Umständen mit 24 multiplizieren.
Zum Eingeben von Datum und Zeit muss man nicht selbst rechnen, das kann die Tabellenkalkulation besser. Geben Sie ein Datum mit 2 Minuszeichen ein, z.B. "31-4-2001" (→ Automatische Zahlenformatierung )-
Übung "Alter in Tagen und Stunden berechnen"
Berechnen Sie Ihr Alter in Tagen, Minuten und Sekunden.
Lösungshinweise mit Musterlösung: PDF, LibreOffice, Excel97 .
4.6.4 Fehlermeldungen
(→ Fehlermeldungen )
⇑ ↑ 4.7 Format übertragen ↓ ⇓
Animation: Übertragen einer
Formatierung mit Hilfe des Pinsels
Harte Formate kann man mit Hilfe des Pinsels von einer Musterzelle auf andere Zellen zu übertragen (OpenOffice erst ab Version 2.0).
- Musterzelle anklicken (Text 1)
- Pinselsymbol anklicken
- Neue Zelle anklicken (Text 2)
Für größere Projekte sollte man mit weichen Formatierungen arbeiten (→ Formatvorlagen ).
⇑ ↑ 4.8 Zellschutz ↓ ⇓
Zellschutz verhindert, dass der Inhalt von Zellen versehentlich oder absichtlich geändert oder auch nur eingesehen werden kann. Dazu kann ein Passwort vergeben werden. Es sind zwei Schritte notwendig:
| Übersicht über die Funktionen | OpenOffice / StarOffice | MS Excel |
|---|---|---|
| Zelle sperren / entsperren | Format - Zelle - Zellschutz - Gesperrt | Format - Zellen - Schutz - Gesperrt |
| Zellschutz aktivieren / deaktivieren mit Passwort | Extras - Dokumentschutz - Tabelle / Dokument | Extras - Schutz - Blatt / Arbeitsmappe |
- Die Zellen, die geschützt werden sollen, müssen gesperrt formatiert werden
- Der Zellschutz für das ganze Tabellenblatt muss aktiviert werden, dabei kann ein Passwort vergeben werden
Übungen

Übung Zeiterfassung
Tipp I : Planen Sie einen ausreichend großen Eingabebereich, und markieren Sie ihn, damit Sie ihn wieder finden. Legen Sie alle Formeln so aus, dass Sie für den ganzen Eingabebereich gelten.
Wie man einen Bereich nachträglich erweitert, finden Sie bei Tabelle erweitern .
Tipp II : Auf Papier sind wir es gewohnt, dass die Ergebnisse einer Rechnung ganz unten stehen. Das hat sich entwickelt, weil man so leichter addieren kann, und ist kein Problem, weil Papierseiten meist klein und übersichtlich ist, seitdem Papyrusrollen nicht mehr üblich sind.
Bei Tabellenkalkulationen ist dies anders. Die Blätter können sehr lang sein, und addieren muss man auch nicht mehr selbst. Deshalb sollten in Tabellenkalkulationen die Ergebnisse immer oben auf dem Blatt stehen, damit man sie auf dem eingeschränkten Ausschnitt des Bildschirmes gleich finden kann.
Übung " Zeiterfassung "
Erstellen Sie eine Liste zur Zeiterfassung, z.B. um wechselnde Arbeitszeiten aufzuschreiben und zu berechnen.
Eingabewerte: Datum, Anfangszeit und Endezeit für jeden Einsatz (grüne Felder)
Zwischenrechnung: Dauer (weißer Felder)
Ausgabewerte: Zeitraum (erstes und letztes Datum) und Gesamtanzahl aller gearbeiteten Stunden (braune Felder).
Lösungshinweise mit Musterlösung: PDF, LibreOffice, Excel97 .
⇑ ↑ 5 Kopiertechniken ↓ ⇓
Die Stärke von Tabellenkalkulationen liegt nicht bei kleinen Währungsrechnern, sondern bei serienweisen Berechnungen, Tabellen mit wechselnden Eingangsdaten, iterativen Berechnungen usw. Um diese Stärken ausnutzen zu können, sollte man bei der Anlage von Tabellenblättern etwas vorausplanen (→ Umfangreiche Tabellen anlegen ):
- Eingangsdaten als Variable eingeben, damit sie geändert werden können ohne in Formeln einzugreifen.
- Blätter in Tabellenform, d.h. als als rechteckige Matrix anlegen, damit die Formeln kopiert werden können und nicht einzeln manuell eingeben werden müssen.
- Auf relative und absolute Adressierung achten, um die Variablen sinnvoll kopieren zu können.
Übung Artikelliste
Legen Sie eine Liste beliebiger Artikel mit einem Nettopreis an. Der Bruttopreis mit Mehrwertsteuer soll von der Tabellenkalkulation berechnet werden. (→ Musterlösung )
Die empfohlene Vorgehensweise wird am Beispiel "Artikelliste" erläutert.
Mit ihr kann man genausogut 40000 statt 4 Artikel bearbeiten - abgesehen vom Eintippen der Artikel und Nettopreise: -)
⇑ ↑ 5.1 Kopieren mit und ohne Listen ↓ ⇓
Nummerieren Sie die Artikelliste.
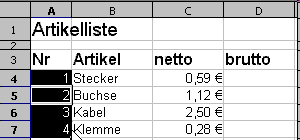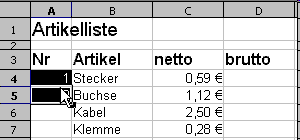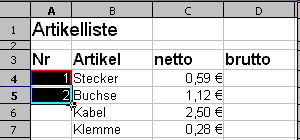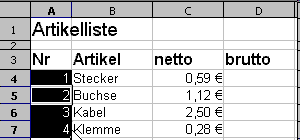
Animation: Nummerieren durch Kopieren
Eine Methode zur Nummerierung ist das Kopieren einer Liste. Gehen Sie dazu wie folgt vor:
- Geben Sie die ersten Zahlen der Nummerierung in die entsprechenden Zellen ein. Hier sind es die Zahlen 1 und 2 in den Zellen A4 und A5.
- Aktivieren Sie die Zellen A4 und A5, indem Sie mit gedrückter linker Maustaste darüber fahren.
- Lassen Sie danach die Maustaste wieder los.
- Fahren Sie jetzt mit der Maus über das rechte untere Eck des markierten Bereiches. Sobald der Mauszeiger wie ein Kreuz aussieht, können Sie die Ecke packen und mit gedrückter linker Maustaste nach unten ziehen.
- Die Tabellenkalkulation versucht, den Rythmus der vorgegebenen Zahlen zu erkennen und fortzusetzen. Manchmal ist es nötig, mehr als zwei Zahlen vorzugeben.
- Wenn man keine Fortsetzung der Liste möchte, sondern wirklich nur kopieren, dann genügt es, die Strg-Taste zu drücken, während man die Zelle kopiert.
Tipp : Mit diesem Verfahren kann man auch andere Listen erzeugen, z.B.
- 1; 3 -->1; 3; 5; 7; 9;.. (ungerade Zahlen)
- Mo; Di -->Mo; Di; Mi; Do; Fr; Sa; So (Wochentage)
- Probieren Sie aus, was Ihre Tabellenkalkulation kann!
⇑ ↑ 5.2 Kopieren mit relativen Adressen ↓ ⇓
Geben Sie in die Zelle D4 die Formel zur Berechnung des Bruttopreises ein, und kopieren Sie die Formel genauso wie oben.
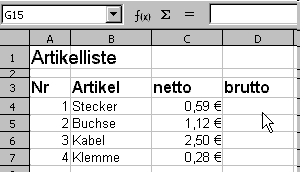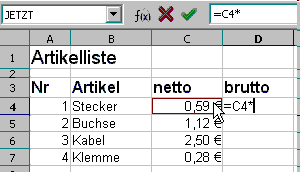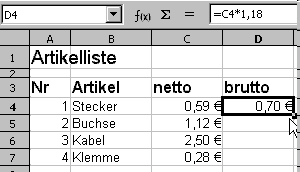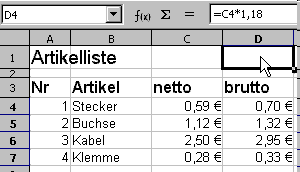
Animation: Formel eingeben und kopieren
(Die MwSt ist leider zu niedrig angegeben)
- Zelle D4 aktivieren
- Formel mit einem Gleichheitszeichen beginnen. Die Rechenleiste verändert sich.
- In die Zelle C4 klicken oder "C4" eintippen, um die Zelle C4 als Variable in die Formel einzufügen. Die Formel rechnet nun mit dem Inhalt der Zelle C4.
- Formel vervollständigen: D4: =C4*1,19
- Formel mit dem grünen Häkchen oder der Return-Taste abschließen
- Rechte untere Ecke der Zelle packen, sobald der Mauszeiger wie ein Kreuz aussieht, und nach unten ziehen
In der Zelle D4 wird das Ergebnis der Berechnung angezeigt. Da die Zelle aktiviert ist, wird die Formel in der Rechenleiste angezeigt.
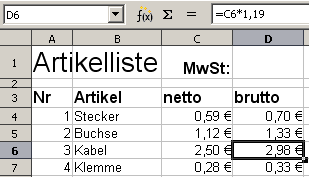
Screenshot: Formel mit relativer Adressierung
Wenn man die neue Formel in D6 prüft, stellt man fest, dass dort nicht die ursprüngliche Formel D4: =C4*1,19 steht, sondern die Formel beim Kopieren angepasst wurde in D6: =C6*1,19.
Begründung : Die Angabe C4 in der Formel D4: =C4*1,19 ist eine relative Adresse .
Anders formuliert, speichert das Programm die Adresse nicht absolut: "Hole den Inhalt aus der Zelle C4", sondern relativ: "Hole den Inhalt aus der Zelle links neben dir". Die zweite Formulierung wird beim Kopieren beibehalten, deshalb holt jede Formel in den Zellen D5, D6 und D7 die Variable aus den Zellen jeweils links daneben. Das nennt man relativ.
So wird es möglich, dass dieselbe Formel mit immer neuen Variablen rechnet. Die Formel muss nur einmal eingegeben werden und kann durch Kopieren vervielfältigt werden.
⇑ ↑ 5.3 externe Variable ↓ ⇓
Die nächste Erhöhung der Mehrwertsteuer kommt bestimmt! Zu allem Ärger müsste dann auch noch die Formel in den Zellen D4 bis D7 der Artikelliste geändert werden. Das ist sehr umständlich, deshalb legt man den Mehrwertsteuersatz besser als externe Variable an, hier in der Zelle D2.
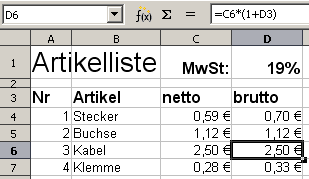
Mehrwertsteuer als externe Variable
in der Zelle D1, aber noch falsch adressiert.
Zahlen, die man unter Umständen ändern muss, sollte man nicht direkt in Formeln schreiben, sondern als externe Variable in einer Zelle ablegen. Die Formel kann sich die Variable aus der Zelle holen, deren Inhalt leicht zu ändern ist ohne Gefahr für die Formel.
Dabei gibt es ein Problem: Wenn man hier die relative Adresse D1 für den Mehrwertsteuersatz verwendet und die Formel D4: = C4*(1+D1) kopiert, ändert sich die ursprüngliche Adresse D1 in den kopierten Formeln und zeigt nicht mehr auf den Mehrwertsteuersatz.
Im Bild steht in der Zelle D6 die Formel D6: = C6*(1+D3) ohne Bezug zum Mehrwertsteuersatz im Feld D1. Diese Formel rechnet Unsinn!
Aus diesen Gründen darf hier die Mehrwertsteuer keine relative Adresse erhalten, sondern es muss eine absolute Adresse sein. Sie wird mit Dollar-Zeichen geschrieben und lautet $D$1.
⇑ ↑ 5.4 Kopieren mit absoluter Adresse ↓ ⇓
Adressieren Sie die externe Variable absolut mit $-Zeichen in der Adresse, und kopieren Sie die Formel.
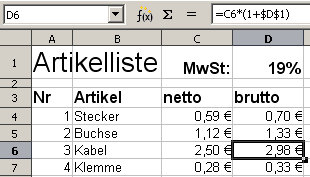
Mehrwertsteuer als externe Variable
in D1 mit absoluter Adressierung $D$1
Absolute Adressen verändern sich beim Kopieren nicht. Man erzeugt sie durch ein $-Zeichen (Dollar) vor dem Buchstaben (Spalte wird festgenagelt) oder vor der Zahl (Zeile wird festgenagelt) oder beiden (Adresse ist komplett festgenagelt).
Die neue Formel in D4 lautet jetzt also: D4: = C4 * (1 + $D$1)
Im Bild kann man in Zelle D6 erkennen, dass die absolute Adresse $D$1 beim Kopieren beibehalten wurde und die Mehrwertsteuer an der korrekten Stelle sucht. Die absolute Adresse $D$1 verweist in jeder kopierten Zelle auf $D$1 und damit auf eine feststehende externe Variable.
Für externe Variable sollten also absolute Adressen gewählt werden, für Laufvariable sind in der Regel relative Adressen günstiger, im Einzelfall auch kombinierte Adressen (siehe folgendes Kapitel).
Tipp : Man muss die $-Zeichen für die absolute Adressen nicht eintippen. Es genügt, in der Rechenleiste die Adresse, z.B. C4, zu markieren und dann mehrmals den Shortcut Umschalt-F4 (OpenOffice) bzw. nur F4 (Excel) zu drücken.
Übung

Preisliste mit 2 Währungen
Übung " Preisliste "
Erstellen Sie für ein Straßenfest eine Preisliste. Geben Sie die Preise in 2 Währungen (€, sfr) an, der Wechselkurs soll leicht veränderbar sein.
Eingabewerte: Artikel, €-Preise und Wechselkurs.
Ausgabewerte: Preise in Schweizer Franken.
Lösungshinweise und Musterlösung: PDF, OpenOffice2, Excel97 . Die Musterlösungen enthalten auch die Lösungen zur Artikelliste.
Hinweis: Ich habe es bisher nicht geschafft, die Grafik aus der Tabellenkalkulation in die PDF-Datei zu retten.
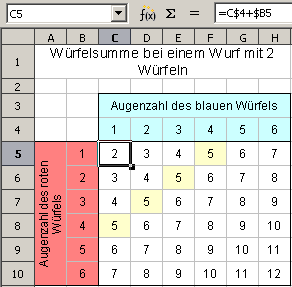
Würfelsummen bei einem Wurf mit 2 Würfeln
Es kann auch nötig sein, innerhalb einer Variablenadresse relative und absolute Adressierung zu mischen, d.h. die Zeile absolut und die Spalte relativ zu adressieren oder umgekehrt.
Im Bild werden die Summen zweier verschiedenfarbiger Würfel in allen möglichen Kombinationen gebildet. Hervorgehoben ist die Zelle C5 mit der Formel =C$4 + $B5.
Für den blauen Würfel oben muss die Adressierung C$4 lauten, damit die absolute Zeilenadresse $4 beim Kopieren nach unten auf der Zeile 4 stehen bleibt, während die relative Spaltenadresse C beim Kopieren nach rechts mitwandern kann. Für den roten Würfel links in $B5 ist es umgekehrt.
Tipp : Man muss die $-Zeichen für die absolute Adressen nicht eintippen. Es genügt, in der Rechenleiste die Adresse, z.B. C4, zu markieren und dann mehrmals den Shortcut Umschalt-F4 (OpenOffice) bzw. nur F4 (Excel) zu drücken.
Übung " Würfelsumme "
Wenn man die Wahrscheinlichkeit berechnen will, 5 Punkte mit zwei Würfeln zu werfen, muss man die Anzahl der Möglichkeiten, 5 Punkte mit 2 Würfeln zu erreichen, durch die Anzahl aller Möglichkeiten teilen. Das Ergebnis ist also 4/36 = 1/9.
Um alle Möglichkeiten von 2 Würfeln darzustellen, bietet sich die Darstellung in einer Matrix 6x6 an.
Erstellen Sie diese Matrix nach dem Muster. Damit Sie die Formel in C5 kopieren können, müssen Sie absolute und relative Adressierungen mischen.
Die Lösung finden Sie im Blatt " Großes 1x1 " (siehe unten).
Übungen
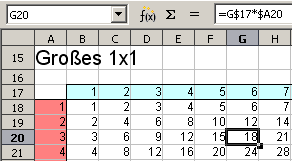
Das große Einmaleins kann
in 60 Sekunden erstellt werden.
Die Übung "Großes 1x1" ist eine bloße Wiederholung der Übung "Würfelsumme".
Übung " Großes 1x1 "
Erstellen Sie eine Matrix mit dem großen Einmaleins bis 20
Musterlösung: PDF ), LibreOffice, Excel97 .
Die Musterlösungen enthalten auch die Lösungen zur Würfelsumme.
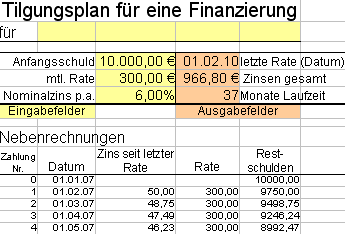
Überschlagen Sie eine Finanzierung
Diese Übung ist das Kernstück meines Kurses
Die Übung "Tilgungsplan" ist das Kernstück dieses Kurses. Begründung:
- Die wesentlichen Teile der Übung, einfache Formeln und Kopiertechniken, sind beim aktuellen Stand des Kurses reine Wiederholung.
- Mit zwei einfachen Formeln und geschicktem Kopieren wird das Tabellenblatt zu einem praktischen Werkzeug. Im Prinzip kann man schon nach 10 Minuten herumprobieren, wie viel und wie lange man für ein Auto oder ein Haus zahlen muss, was eine Finanzierung kostet usw. Meines Erachtens ist das nicht schädlich für junge Menschen voller Konsumgelüste.
- Das geschickte Kopieren basiert auf einer geeigneten Anordnung des Blattes und auf relativer und absoluter Adressierung. Diese müssen Sie verstanden haben, sonst zurück, marsch, marsch .
- Die mystische Zinseszinsberechnung wird auf einfache Formeln, die fast alle Schüler verstehen, und häufige Wiederholung reduziert. Dies ist ein Beispiel für numerische statt analytischer Lösungsmethoden.
Vielleicht werden damit einige junge Menschen für die Mathematik und die Ingenieurwissenschaften gewonnen. - WeitereElemente der Übung "Tilgungsplan" wie Laufzeit, grafische Darstellung usw. sind Kosmetik, dienen nur dem Komfort und sind nicht unbedingt für die Funktion des Blattes erforderlich. Sie bieten aber die Überleitung für eben dieseElemente.
Übung " Tilgungsplan "
Erstellen Sie einen Tilgungsplan, mit dem Sie überschlagen können, wie lange Sie an Ihren Schulden zu knabbern haben, wenn Sie die Finger nicht davon lassen können.
Arbeitsblatt: PDF mit ausführlicher, aber älterer Arbeitsanleitung
Musterlösung: PDF, OpenOffice3 (LibreOffice stellt die Kommentare scheußlich dar, aber sonst funktioniert es), Excel97 .
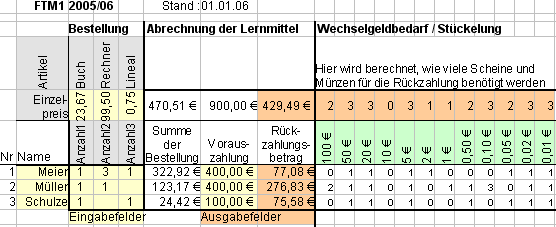
Sammelbestellung
Wichtiger Hinweis : Auch Tabellenkalkulationen können sich verrechnen!
Im Tabellenblatt Sammelbestellung wird die Funktion =GANZZAHL() verwendet, um Kommastellen abzuschneiden. Dies ist bei der Ermittlung des Wechselgeldbedarfes notwendig, weil nur ganze Scheine ausgegeben werden sollen: -)
Die Funktion =GANZZAHL() kann zu Fehlern führen. Warum das so ist, und wie Sie das Problem lösen, finden Sie in der Arbeitsanweisung zur Sammelbestellung und im Kapitel numerische Fehler .
Tipp : Natürlich ist das Eingabefeld der Sammelbestellung viel zu klein. Wie Sie es erweitern können, finden Sie im Kapitel Tabellen erweitern .
Übung " Sammelbestellung "
Erstellen Sie ein Tabellenblatt, mit dem eine Sammelbestellung erfasst und abgerechnet werden kann. Außerdem soll der Wechselgeldbedarf mit der nötigen Anzahl von Scheinen und Münzen ermittelt werden.
Arbeitsblatt: PDF (16kB) mit ausführlicher Arbeitsanleitung
Musterlösung: PDF, LibreOffice, Excel97 .
⇑ ↑ 6 Arbeiten mit Funktionen ↓ ⇓
Mit Funktionen kann man alle erdenklichen Berechnungen durchführen und auch Texte manipulieren.
Sie können übrigens alle Funktionen, die hier als Beispiel aufgeführt sind, aus der Webseite kopieren, in eine Zelle einer Tabellenkalkulation einfügen und das Ergebnis prüfen.
⇑ ↑ 6.1 Aufbau von Funktionen ↓ ⇓
Alle Funktionen in Tabellenkalkulationen beginnen mit einem Gleichheitszeichen, dann folgt die Bezeichnung der Funktion (außer bei einfachen Grundrechenarten) und zuletzt die Liste der Argumente in Klammern.
- =WURZEL(17)
berechnet die Quadratwurzel aus der Zahl 17
Bei einfachen Grundrechenarten kann die Angabe der Funktion entfallen, muss aber nicht.
- =2*3
- =PRODUKT(2;3)
berechnen beide das Produkt der Zahlen 2 und 3 mit dem Ergebnis 6
Auch bei Funktionen ohne Argumente folgen (leere) Klammern:
- =PI()
π= 3,1415.. - =JETZT()
gibt die aktuelle Uhrzeit an - =HEUTE()
Argumente können relative oder absolute oder gemischte Adressen sein.
- =SIN(C5)
- =TAN(C$5)
- =ARCCOS($C$5)
berechnen die angegebene Winkelfunktionen für den Wert aus der adressierten Zelle C5
Winkelfunktionen und ihre Umkehrfunktionen (trigonometrische und zyklometrische Funktionen) rechnen mit dem BogenmaßRAD. Beim Bogenmaß steht 2 π für einen Vollkreis von 360°, bzw. π für einen halben Kreis von 180°.
Wenn man Winkelfunktionen mit Winkelgrad DEG (360°) rechnen möchte, muss man die Winkelgrade ins Bogenmaß umwandeln. Das geht mit der Funktion =RAD(Winkelgrad) oder altmodisch, indem man die Winkelgrad mit π multipliziert und durch 180° teilt.
Umgekehrt verwendet man die Funktion =DEG(Bogenmaß) oder rechnet altmodisch (siehe Beispiel rechts).
- =SIN(RAD(30°))
=SIN(30 * PI() / 180)
berechnen den Sinus des Winkels 30°, das Ergebnis ist 0,5. - =DEG(ARCTAN(0,5))
=ARCTAN(0,5)*180/PI()
berechnen den Arcustangens von 0,5 und gibt das Ergebnis 26,56 in Winkelgrad aus. Die Einheit ° muss man sich dazu denken.
Wenn eine Funktion mehrere Argumente benötigt, werden diese durch Strichpunkte getrennt. Die Reihenfolge der Argumente ist fest vorgegeben, man kann sie in der Hilfefunktion nachschlagen. Wenn man Formelassistenten zur Erstellung der Formel verwendet, wird die Reihenfolge automatisch eingehalten.
- = WENN (A5>A6; A5; A6)
prüft, welche der Zellen A5 und A6 den größeren Inhalt hat, und zeigt die größere Zelle an.- WENN: Das erste Argument A5>A6 stellt die Frage, ob der Zellinhalt von A5 größer als der von A6 ist, und gibt ein eindeutiges Ergebnis: WAHR oder FALSCH bzw. in Zahlen 1 oder 0
- DANN: Das zweite Argument A5 wird ausgeführt, wenn die Bedingung im ersten Argument WAHR ist, d.h. A5 größer als A6 ist. In diesem Fall wird der Zellinhalt von A5 angezeigt.
- SONST: Das dritte Argument A6 wird ausgeführt, wenn die Bedingung im ersten Argument nicht wahr (FALSCH) ist, d.h. A6 größer oder gleich A5 ist. In diesem Fall wird der Zellinhalt von A6 angezeigt.
Manche Funktionen verwenden eine unbestimmte Anzahl von Argumenten. Da in solchen Fällen die Argumente gleichwertig sind, spielt ihre Reihenfolge keine Rolle.
- =MAX(A5;A6)
liefert dasselbe Ergebnis wie die =WENN()-Funktion im vorhergehenden Beispiel - =PRODUKT(2;3;C7;5;C12)
berechnet das Produkt aus den Zahlen 2,3 und 5 und den Zellinhalten aus C7 und C12.
Als Argumente können auch ganze Bereiche angegeben werden. Diese rechteckigen Bereiche werden mit zwei Zelladressen und einem Doppelpunkt dazwischen bezeichnet. Um diese Bereiche einzugeben genügt es, die Bereiche mit der Maus zu markieren.
- =SUMME(D1: F3)
berechnet die Summe aller Zellen, die im Rechteck zwischen D1 und F3 liegen. - =Mittelwert(Tabelle2.D3: Tabelle5.D3)
ermittelt den Mittelwert der Zellen D3 in den Tabellenblätter 2 bis 5 und gibt ihn aus.
⇑ ↑ 6.2 Operatoren ↓ ⇓
Operatoren sind Sonderzeichen, die innerhalb von Formeln verwendet werden. Man unterscheidet arithmetische Operatoren, Textoperatoren, Vergleichsoperatoren, Bezugsoperatoren und Boolesche Operatoren.
Arithmetische Operatoren
sind die üblichen Rechenzeichen + (plus), - (minus), * (mal), / (geteilt durch), ^ (hoch) und % (Prozent).
Das Hoch-Zeichen ^ erscheint am Bildschirm erst, wenn eine weitere Taste gedrückt wird: -)
- = 2 + 3
berechnet die Summe 2 plus 3 = 5 - = -2 - 3
berechnet die Differenz (-2) minus 3 = (-5) - = 2 * 3
(Sternchen) berechnet das Produkt 2 mal 3 = 6 - = 2 / 3
berechnet die Division 2 geteilt durch 3 = 0,66.. - = 2 ^ 3
berechnet die Potenz 2 hoch 3 = 8 - = 20%
rechnet in Prozent um 20%= 0,20 (teilt durch 100)
Textoperatoren
dienen den Umgang mit Texten (Strings). Textoperatoren sind das kaufmännische UND & und die Anführungszeichen ".
- &
Das kaufmännische UND setzt Texte zusammen. - "
Alles, was zwischen Anführungszeichen steht, wird als Text behandelt.
- = "Name" & ", " & "Vorname"
in Anführungszeichen " " gesetzte Zeichen werden als Text behandelt, das kaufmännische UND & reiht Texte aneinander.
Das Ergebnis ist "Name, Vorname" (ohne Anführungszeichen).
Eine merkwürdige Verwendung des kaufmännischen UND & finden Sie im folgenden Beispiel. Beide Formeln produzieren in OOo2.3 dasselbe Ergebnis, aber eine Übertragung auf ähnliche Beispiele ist mir bisher nicht gelungen.
- =WENN(D19&D20&D21=""; "wahr";"falsch")
- =WENN(UND(D19="";D20="";D21=""); "wahr";"falsch")
Vergleichsoperatoren
sind die Zeichen = (gleich), > (größer als), >= (größer oder gleich), < (kleiner als), <= (kleiner oder gleich) und <>: (ungleich).
Sie vergleichen zwei Werte und geben das Ergebnis WAHR bzw. 1 oder das Ergebnis FALSCH bzw. 0. Vergleichsoperatoren werden oft in der Wenn-Funktion eingesetzt, aber auch in anderen Funktionen.
- = A5 > 3
Wenn der Inhalt der Zelle A5 größer als 3 ist, ist das Ergebnis des Vergleiches WAHR, ansonsten FALSCH.
In diesem Beispiel ist der Vergleichsoperator das Zeichen >, aber sinngemäß funktioniert es auch mit jedem anderen Vergleichsoperatoren. - =WENN(A5 > 3; "A5 ist größer"; " A5 ist kleiner oder gleich" )
Im 1. Argument steht der Vergleich, hier "Inhalt der Zelle A5 größer als 3".
Wenn der Vergleich WAHR ist, wird das 2. Argument "A5 ist größer" ausgegeben.
Wenn der Vergleich FALSCH ist, wird das 3. Argument "A5 ist kleiner oder gleich" ausgegeben.
Bezugsoperatoren
verwendet man, wenn für Argumente ganze Bereiche verwendet werden. Bezugsoperatoren sind der Doppelpunkt, der Strichpunkt (Semikolon) und das Leerzeichen.
- Bereichsoperator:
- = ANZAHL(C1: C1000)
gibt die Anzahl aller Zahlenwerte im adressierten Bereich C1 bis C1000 aus. Zellen, die Text enthalten oder leer sind, werden nicht gezählt. - = ANZAHL2(B3: C5)
gibt die Anzahl aller belegten Zellen (Zahl oder Text) im adressierten Bereich aus - = PRODUKT(B2: C4)
berechnet das Produkt aller Zellen im rechteckigen Bereich B2 bis C4 =B2*B3*B4*C2*C3*C4
- = ANZAHL(C1: C1000)
- Vereinigungsoperator;
- = SUMME(B2: C3; F4: G6)
berechnet die Summe aller Werte in den beiden rechteckigen Bereichen.
- = SUMME(B2: C3; F4: G6)
- Schnittmengenoperator (Leerzeichen)
- = SUMME(A1: C1 B1: D1)
berechnet die Summe aus den Zellinhalten, die sowohl in dem einen als auch dem anderen rechteckigen Bereich liegen. Das sind in diesem Falle die Zellen B1 und C1.
- = SUMME(A1: C1 B1: D1)
Boolesche Operatoren
werden in Tabellenkalkulation gar nicht durch Operatoren, sondern durch (logische) Funktionen realisiert.
- =UND(3=2+1;5>2)
liefert WAHR, wenn jedes Argumente WAHR sind, in diesem Fall ja. Es können auch mehr als zwei Argumente verwendet werden. - =ODER(4=2+1;5<2)
liefert WAHR, wenn eines der Argumente WAHR ist, in diesem Fall nicht. Es können auch mehr als zwei Argumente verwendet werden. - =NICHT(5>2)
liefert das Gegenteil des Ergebnisses, in diesem Fall FALSCH. - =WENN(A5 > 3; "A5 ist größer"; " A5 ist kleiner oder gleich" )
Wenn der Vergleich im 1. Argument der Wenn-Funktion WAHR ergibt, wird das 2. Argument ausgeführt und "A5 ist größer" ausgegeben. Bei FALSCH wird das 3. Argument ausgeführt und "A5 ist kleiner oder gleich" ausgegeben.
⇑ ↑ 6.3 Eingabe von Formeln bzw. Funktionen ↓ ⇓
Funktionen können auf zwei Arten eingeben werden:
- entweder mit dem Formelassistenten
- oder in der Funktionsleiste (Rechenleiste)
6.3.1 Eingabe einer Formel durch Eintippen
Einfache Formeln tippt man am schnellsten über die Tastatur ein.
Animation: Formel eintippen
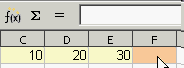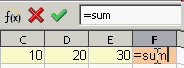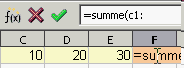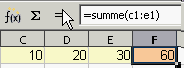
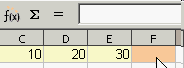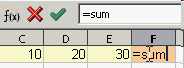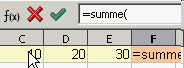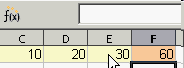
- Zelle F1 aktivieren.
- Formel über die Tastatur eintippen.
F1: =summe(c1: e1)
Die Formel kann man in der Funktionsleiste und in der Zelle bearbeiten, Groß- und Kleinschreibung spielt keine Rolle. - Formel abschließen mit einem Klick auf das grüne Häkchen (oder durch Drücken der Return-Taste).
Nach dem Klick auf das grüne Häkchen bleibt die Formel in der Funktionsleiste sichtbar, während in der Zelle F1 das Ergebnis der Berechnung erscheint.
6.3.2 Erleichterung der Eingabe durch das Markieren von Bereichen
Adressen von einzelnen Zellen oder ganzen Zellbereichen muss man nicht eintippen. Es genügt, in die Zelle zu klicken oder über den gewünschten Zellbereich mit gedrückter linker Maustaste zu fahren.
Animation: Formel
eintippen mit der
Bereichsmarkierung.
- Zelle F1 aktivieren.
- Formel bis zu geöffneten Klammer über die Tastatur eintippen.
F1: =summe( - Mit gedrückter linker Maustaste über die Zellen C1, D1 und E1 fahren.
Die Adressen der überfahrenen Zellen werden in die Formel aufgenommen.
F1: =summe(C1: E1 - Die Klammer muss per Tastatur geschlossen werden.
F1: =summe(C1: E1) - Durch das Drücken der Return-Taste springt der Mauszeiger in die nächste Zelle, deshalb ist die Formel nicht mehr in der Funktionsleiste zu sehen. In der Zelle F1 wird das Ergebnis der Berechnung angezeigt.
Tipp : In der Animation springt der Mauszeiger in die Zelle unter C1. Die Richtung, in die der Mauszeiger springt, kann man einstellen. Dies ist praktisch, wenn man längere Datenkolonnen eintippen muss.
- OpenOffice 2: Extras - Optionen - OpenOffice Calc - Allgemein - Eingabebestätigung setzt die Selektion nach….
- MS Excel 97: Extras - Optionen - Bearbeiten - Markierung nach dem Drücken der Eingabetaste verschieben nach…
6.3.3 Eingabe einer Formel mit dem Funktionsassistenten
Übung "6 Richtige im Lotto"
Um die Wahrscheinlichkeit für 6 Richtige im Lotto zu berechnen, kann man die hypergeometrische Funktion verwenden. Sie benötigt 4 Argumente. Im Falle Lotto sind dies:
- N = 49 Kugeln in der Lostrommel
- d = 6 Kugeln haben wir auf dem Tippzettel angekreuzt und wollen sie jetzt gezogen sehen.
- n = 6 sind die Kugeln, die tatsächlich gezogen werden.
- x = 6 Richtige interessieren uns im Moment. Wer die Wahrscheinlichkeit für 5 Richtige wissen möchte, schreibt hier eine 5.
Da man selten auswendig weiß, welche Argumente in welcher Reihenfolge angegeben sein müssen, ist es zweckmäßig, den Formelassistenten zu verwenden.
Komplizierte und selten benutzte Formeln gibt man besser mit dem Funktions-Assistenten ein. Dann muss man sich nicht merken, welche Argumente in welcher Reihenfolge angegeben sein müssen.
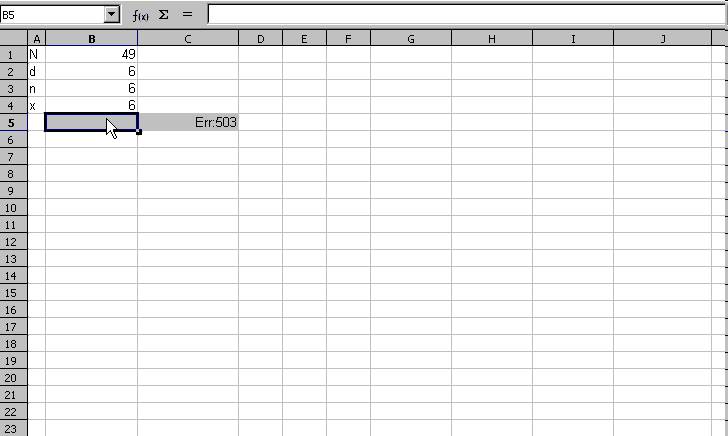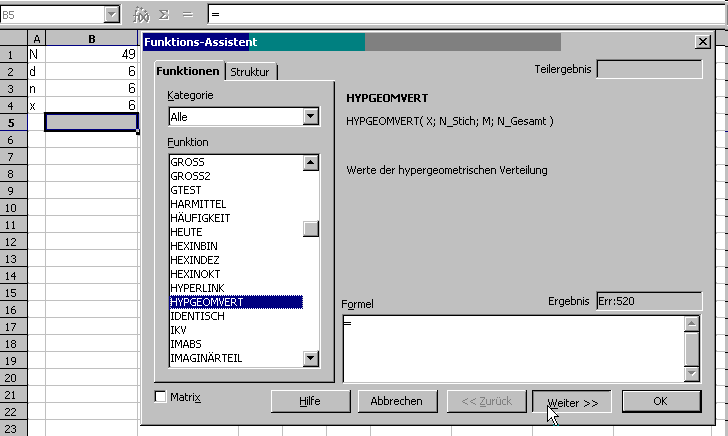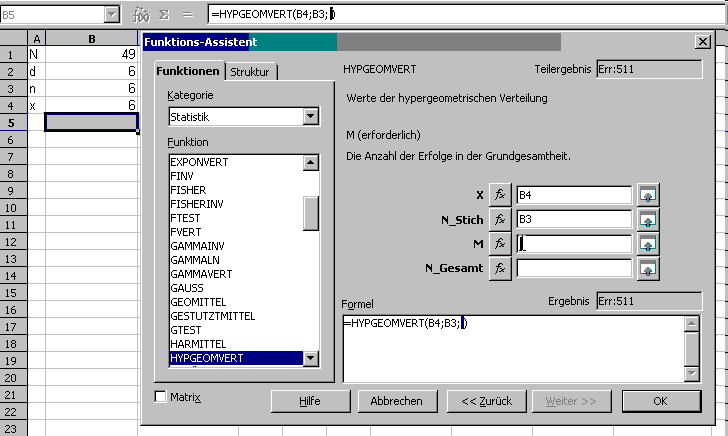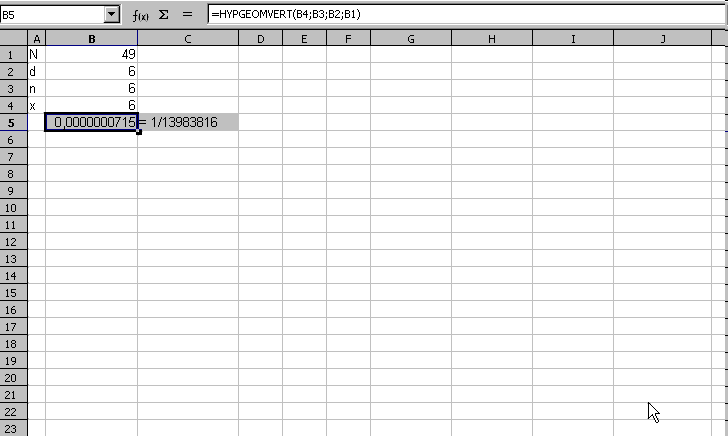
Animation: Hypergeometrische Funktion mit Hilfe des Formelassistenten eingeben.
Der Kehrwert 1/13 Mio wurde zusätzlich programmiert.
- Klicken Sie die Zelle B5 an, in der die Formel stehen soll.
- Öffnen Sie den Funktions-Assistenten durch Klick auf das Zeichen f(x).
- Wählen Sie die hypergeometrische Funktion =HYPGEOMVERT()
- Wählen Sie "Weiter"
- Klicken Sie im Funktions-Assistenten in das Eingabefeld x, damit die nächste Eingabe dorthin gelangt. Es erscheint ein Hilfetext - wohl dem, der die manchmal geheimnisvollen Texte versteht.
- Klicken Sie anschließend im Tabellenblatt in die Zelle B4.
Die Adresse B4 wird in die Funktion übernommen. Die Übernahme kann man im Eingabefeld x, im Funktionsassistenten bei "Formel" und in der Rechenleiste beobachten. - Verfahren Sie genauso mit den anderen Argumenten. Natürlich können Sie die Zelladressen oder Werte auch in den Eingabefeldern des Funktionsassistenten eingetippen.
- Sobald genügend Werte eingegeben sind, erscheint das Ergebnis für die vorliegenden Zahlen im Funktionsassistenten.
- Schließen Sie die Eingabe der Funktion mit OK ab.
Als Ergebnis wird meist 0 angezeigt, aber das ist nur falsch gerundet. Das richtige Ergebnis lautet 1 zu 13'983'816 (Wahrscheinlichkeit für 6 Richtige im Lotto). Formatieren Sie das Ergebnis so, dass Sie einen brauchbaren Zahlenwert ablesen können, und überprüfen Sie den Zahlenwert: Natürlich benötigt man keinen Taschenrechner, um den Kehrwert zu berechnen, wenn man vor einer Tabellenkalkulation sitzt: -).
Man könnte die Formel auch direkt in die Zelle B5 eintippen, sie muss lauten
- =HYPGEOMVERT(6;6;6;49)
Weder in den Tabellenkalkulationen noch in der Statistik gibt es einheitliche Bezeichnungen für die Argumente der hypergeometrischen Verteilung. Deshalb folgt hier ein Überblick:
| Wert | Zahlenwert beim Lotto | Abkürzung in Excel 97 | Abkürzung in OpenOffice / StarOffice | Abkürzung in meinem Statistikkurs |
|---|---|---|---|---|
| Anzahl der gesuchten Erfolge | 6 | Erfolge_S | X | x |
| Stichprobenumfang = Anzahl der gezogenen Kugeln (ohne Zusatzzahl) | 6 | Umfang_S | N_Stich | n |
| Anzahl der "richtigen" Kugeln in der Trommel | 6 | Erfolge_G | M | d |
| Gesamtzahl der Kugeln in der Trommel | 49 | Umfang_G = N | N_Gesamt | N |
⇑ ↑ 6.4 Korrigieren einer Formel ↓ ⇓
Eine der größten Schwierigkeiten bei der Arbeit mit Tabellenkalkulationen ist die Suche nach Fehlern in Formeln. Deshalb bieten die Tabellenkalkulationen dazu einige Hilfe an. Wenn man eine Formel eingegeben hat und dann die Formel überprüfen will, macht man einen Doppelklick auf die Zelle, in der die Formel steht. Man hat jetzt folgende Möglichkeiten:
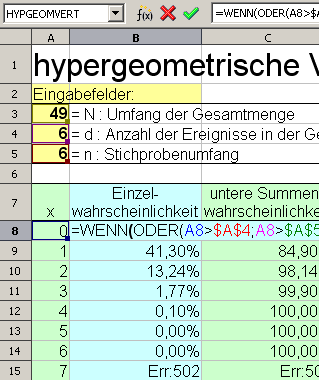
Formel überprüfen:
beachten Sie die farblich
hervorgehobenen Zellen und Klammern.
- Die Formel ist zweimal dargestellt, einmal in der Funktionsleiste / Rechenleiste, ein zweites Mal in der Zelle (hier B8).
- Die Adressen in der unteren Formel und die adressierten Zellen sind farblich markiert, die Zellbezüge können so kontrolliert werden.
Man kann die Formel in der Funktionsleiste / Rechenleiste bearbeiten.
- Hineinklicken
- Bewegen mit Rechts- und Linkspfeil. Beachten Sie, wie zusammengehörigen Klammern kurz hervorgehoben werden, wenn man darüber fährt.
- Zellbezüge können Sie ändern, indem Sie die Adresse neu eintippen. Sie können auch eine falsche Adresse markieren und dann die richtige Adresse anklicken.
- Die Adressierungsart (relativ oder absolut) ändern Sie ebenfalls, indem Sie die $-Zeichen eintippen / löschen oder indem Sie die falsche Adresse markieren und dann die Adressierungsart ändern (mit der F4-Taste bei Excel bzw. [Strg]-F4 bei StarOffice).
- Sie können die komplette Formel in der Funktionsleiste eingeben und ändern. Das hat Vorteile, wenn man sich auskennt und es schnell gehen soll, oder wenn die Formeln stark verschachtelt sind.
- Beenden Sie eine erfolgreiche Formeleingabe, indem Sie das grüne Häkchen anklicken.
- Brechen Sie eine Formeleingabe ohne Ändern ab, indem Sie das rote Kreuz anklicken.
Man kann auch wieder den Formelassistenten aufrufen, indem man "f(x)" anklickt.
Die Beschreibung ist so gehalten, dass sie für Excel 97 und StarCalc / OpenOffice gilt. Tatsächlich bieten StarCalc / OpenOffice weitere Möglichkeiten.
Fehlermeldungen finden Sie im Anhang.
Erweitern Sie die Übung "Lotto" zur Übung "Hypergeometrische Verteilung", in dem auch die Wahrscheinlichkeit für 0,1, … 25 Richtige ermittelt werden. Verwenden Sie das oben stehende Bild als Muster.
Anweisungen und Lösungen finden Sie am Ende des Kapitels bei der Übung " Hypergeometrische Verteilung
⇑ ↑ 6.5 Verschachteln von Formeln ↓ ⇓
Im Bild der Übung "Hypergeometrische Verteilung" (oben) steht in der Zelle B15 eine Fehlermeldung, weil dort versucht wird, die Wahrscheinlichkeit für 7 Richtige im Lotto zu berechnen. Man kann eben eine Wahrscheinlichkeit für x Richtige nur dann berechnen, wenn mindestens x Kugeln gezogen werden (n>=x) UND mindestens x richtige Kugeln in der Lostrommel waren (d>=x).
Die Fehlermeldungen stören nicht nur das Bild des Tabellenblattes, sondern auch die weitere Verarbeitung der Ergebnisse (siehe Zelle C15 im Bild).
Deshalb soll in jeder Zelle zunächst geprüft werden, ob die Voraussetzungen für ein korrektes Ergebnis erfüllt sind, bevor die Wahrscheinlichkeit berechnet wird. Wenn die Voraussetzungen nicht erfüllt sind, soll in der Zelle nichts angezeigt werden.
Dazu sind die folgenden Schritte notwendig:
- Feststellen, ob x größer als n ist.
- Feststellen, ob x größer als d ist.
- Verknüpfen der beiden Feststellungen durch ODER.
- Prüfen, ob x größer als n ODER x größer als d ist.
Wenn ja, wird nichts angezeigt.
Wenn nein, wird das Ergebnis der hypergeometrischen Funktion angezeigt.
Formeln können als Argumente nicht nur Zahlen und Zelladressen enthalten, sondern auch andere Formeln. Das nenne ich verschachtelte Formeln.
Verschachtelte Formeln kann man in der Rechenleiste eintippen oder in neueren Programmversionen mit dem Formelassistenten erstellen. Aber sie können sehr groß und unübersichtlich werden, und die Fehlersuche sehr schwierig. Deshalb empfehle ich, verschachtelte Formeln als Einzelformeln zu erstellen und zu testen, und sie erst dann zusammenzusetzen, wenn sie ausgetestet sind und funktionieren.
Diese Vorgehensweise zum Erstellen verschachtelter Formeln möchte ich hier zeigen.

Formeln verschachteln: 1. Schritt
Schritt 1 : Formel in kleinen Schritten erstellen.
Schritt 1a : Feststellen, ob x größer als n ist.
- Geben Sie in Zelle E8 eine Funktion für die Feststellung ein. Die Funktion lautet in Zelle E8: = A8>A5.
- Geben Sie für n (Zelle A5) eine absolute Adresse mit $-Zeichen ein, damit die Funktion nach unten kopiert werden kann. Die Funktion lautet dann in Zelle E8: =A8>$A$5.
- Die Funktion =A8>$A$5 und ihre Zelladresse E8 können Sie in der Rechenleiste sehen.
- Kopieren Sie die Zelle nach unten.
- Prüfen Sie, ob die kopierten Zellen anzeigen, wann x zu groß ist. Sie tun es hier durch die Anzeige "WAHR".
- Korrigieren Sie die Funktion, falls sie nicht die gewünschten Ergebnisse anzeigt.
Formeln verschachteln: 2. Schritt
Schritt 1b : Verknüpfen der beiden Feststellungen durch ODER.
- Verfahren Sie ähnlich wie im ersten Schritt, diesmal in Spalte F. Die Funktion können Sie dem Bild entnehmen.
Formeln verschachteln: 3. Schritt
Schritt 1c : Verknüpfen der beiden Feststellungen durch ODER.
- Verfahren Sie ähnlich wie im ersten Schritt, diesmal in Spalte G.
- In allen Funktion stehen die Argumente in Klammern und werden durch Strichpunkte getrennt. In der ODER-Funktion spielt die Reihenfolge der Argumente keine Rolle, es können auch mehr als zwei sein.
Formeln verschachteln: 4. Schritt
Schritt 1d : Prüfen, ob x größer als n ODER x größer als d ist.
Wenn ja, wird nichts angezeigt.
Wenn nein, wird das Ergebnis der hypergeometrischen Funktion angezeigt.
- Verfahren Sie ähnlich wie im ersten Schritt, diesmal in Spalte H.
- Auch in der WENN-Funktion stehen alle Argumente zwischen Klammern und werden durch Strichpunkte getrennt. Es gibt immer 3 Argumente:
- Das erste Argument ist die Prüfung, deren Ergebnis WAHR (1) oder FALSCH (0) sein kann. In diesem Fall wird die Prüfung aus der Spalte G übernommen.
- Das zweite und mittlere Argument beschreibt, was geschehen soll, wenn die Prüfung WAHR ergibt. In diesem Fall wird das angezeigt, was zwischen den "Anführungszeichen" steht: nichts.
- Das dritte und letzte Argument beschreibt, was geschehen soll, wenn die Prüfung FALSCH ergibt. In diesem Fall wird der Inhalt der Zelle aus Spalte B übernommen.
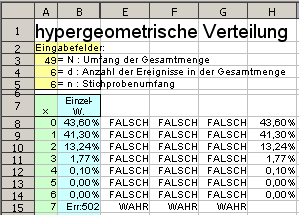
Formeln verschachteln: 5. Schritt
Setzen Sie dies fort, bis alleElemente der Formel vorhanden sind.
Schritt 2 : Prüfen der Funktionen.
- Kopieren Sie alle Formeln nach unten.
- Prüfen Sie die Ergebnisse und korrigieren Sie gegebenenfalls die Formel.
Im Beispiel sieht man die endgültige Anzeige in Spalte H. Im Feld H15 wird wie gewünscht nichts mehr angezeigt.
Jetzt können Sie beginnen, die einzelnen Formeln in einer Zelle zusammenzusetzen.
Schritt 3 : Zusammensetzen der einzelnen Formeln in eine Zelle.
Im Prinzip ist ganz einfach: Ersetzen Sie in den Formeln die Verweise auf andere Formeln durch die anderen Formeln selbst, bis nur noch eine Formel übrig ist. Wichtig ist, dass sich beim Ersetzen die relativen Adressen nicht verändern dürfen. Deswegen sollen nicht Zellen, sondern nur der Formeltext in der Rechenleiste übertragen werden.
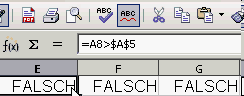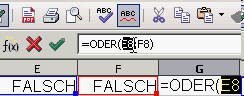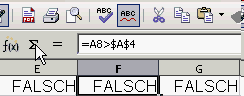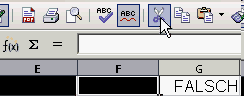
Formeln ineinander einsetzen.
Schritt 3a : E8 und F8 in G8 einsetzen.
- Zelle E8 anklicken
- Formel in der Rechenzeile ohne Gleichheitszeichen markieren und kopieren
- Klick auf das rote Kreuz, um die Zelle ohne Änderung verlassen. Dadurch wird die Formel noch erhalten, falls etwas schief gehen sollte.
- Zelle G8 anklicken
- Adresse E8 markieren
- Einfügen setzt die Formel aus E8 statt der Zelladresse E8 ein.
- Klick auf das grüne Häkchen, um die Änderung zu übernehmen.
- Wie oben: Formel aus F8 in die Formel in G8 einsetzen
- E8 und F8 löschen, die Anzeige in G8 muss erhalten bleiben
Schritt 3b : B8 und G8 in H8 einsetzen.
=WENN(ODER(A8>$A$5;A8>$A$4);"";HYPGEOMVERT(A8;$A$5;$A$4;$A$3))
Schritt 4 : Zelle verschieben.
Im Detail unterscheidet sich das Verschieben in OpenOffice und Excel.
OpenOffice / StarOffice
Formeln verschieben
in OpenOffice / StarOffice
- Mit gedrückter Maustaste über die Zellen fahren, die verschoben werden sollen. Wenn es nur eine Zelle ist, kann man in eine Nachbarzelle und zurück fahren. Anschließend ist der Zellbereich schwarz markiert.
- Maustaste loslassen.
- Zellbereich nochmals IN DER MITTE packen und seinen Inhalt verschieben.
MS Excel
Formeln verschieben
in MS Excel.
- Mit gedrückter Maustaste über die Zellen fahren, die verschoben werden sollen. Anschließend ist der Zellbereich schwarz umrandet.
- Maustaste loslassen.
- Zellbereich nochmals AM RAND packen und seinen Inhalt verschieben.
Übung " Hypergeometrische Verteilung "
Erstellen Sie ein Tabellenblatt zur Untersuchung hypergeometrischer Verteilungen. Es soll nicht nur die Wahrscheinlichkeit für 6 Richtige, sondern für x = 0 bis 25 "Richtige" berechnen.
Eingabewerte: Umfang der Gesamtmenge N, Anzahl der Ereignisse in der Gesamtmenge d, Stichprobenumfang n.
Ausgabewerte für alle mögliche Ereignisse x in der Stichprobe: Einzelwahrscheinlichkeiten, untere und obere Summenhäufigkeiten, Säulendiagramm für die Einzelwahrscheinlichkeiten.
Musterlösung mit Hinweisen: PDF, OpenOffice2, Excel97 .
⇑ ↑ 6.6 Ändern ganzer Tabellenblätter ↓ ⇓
Übung " Binomiale Verteilung "
Aufgabe: Erstellen Sie ein Tabellenblatt zur Untersuchung binomialer Verteilungen, indem Sie das vorhandene Tabellenblatt "Hypergeometrische Verteilung" abwandeln.
Eingabewerte: Anteil der Ereignisse in der Gesamtmenge p, Stichprobenumfang n, mögliche Ereignisse x.
Ausgabewerte für alle mögliche Ereignisse x (bis x=25) in der Stichprobe: Einzelwahrscheinlichkeiten, untere und obere Summenhäufigkeiten, Säulendiagramm für die Einzelwahrscheinlichkeiten
Arbeitsblatt: PDF mit ausführlicher Arbeitsanleitung
Musterlösung: PDF, OpenOffice2, Excel97 .
Wo immer möglich, sollte man neue Tabellenblätter erstellen, indem man ein vorhandenes ähnliches Tabellenblatt kopiert und dann ändert. Dies ist nicht nur eine sehr zeitsparende Strategie, sondert ergibt auch automatisch eine gewisse Ähnlichkeit im Aufbau der Blätter.
Notwendige Arbeitstechniken
- Zeilen löschen und einfügen
- Zellen verschieben
- Formeln korrigieren
⇑ ↑ 7 Diagramme ↓ ⇓
"Ein Bild sagt mehr als tausend Worte", deshalb bieten Tabellenkalkulationen einige Möglichkeiten, Zahlen in Diagrammen darzustellen.
Tabellenkalkulationen zeichnen Diagramme nicht aus Formeln, sondern aus Datenreihen. Die Daten können einigermaßen frei auf dem Tabellenblatt angeordnet werden können, aber um den folgenden Text zu vereinfachen, gehe ich davon aus, dass die Datenreihen in zusammenhängenden Bereichen senkrecht angeordnet sind.
Bei allen äußerlichen Unterschieden gibt es in Tabellenkalkulationen nur zwei Grundtypen von Diagrammen: (→ ausführlicher Vergleich )
- y-Diagramme für (eindeutige) Funktionen bilden eine Reihe von Werten ab.
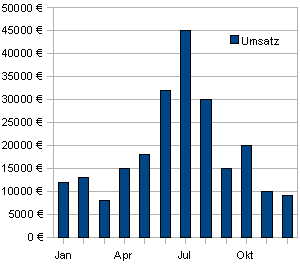
- Typischer Vertreter eines y-Diagrammes ist das Balkendiagramm, das eine oder mehrere Zahlenreihen grafisch darstellt. Für ein y-Diagramm genügt schon eine Datenreihe mit den y-Werten in einer einzigen Spalte. (→ y-Diagramme )
- xy-Diagramme für Relationen (mehrdeutige Funktionen) bilden eine Reihe von Wertepaaren ab.
- Ein xy-Diagramm zeichnet Punkte oder Linien nach Koordinaten. Damit sind - theoretisch - beliebige Linienverläufe möglich. Für ein xy-Diagramm benötigt man x-y-Wertepaare (Koordinaten) in mindestens 2 Spalten. (→ xy-Diagramme )
⇑ ↑ 7.1 y-Diagramm erstellen ↓ ⇓
Für ein y-Diagramm genügt in einer Tabellenkalkulation eine Datenreihe mit den y-Werten in einer einzigen Spalte. Die Werte werden mit gleichmäßigen Abständen in der gelisteten Reihenfolge dargestellt, z.B. als Balken, Tortenstücke o.ä. Falls eine Datenreihe für die x-Werte vorhanden ist, kann sie der Beschriftung der Datenreihe dienen, aber nicht die Abstände der Balken (Skalierung) beeinflussen.
Selbst wenn man ein Liniendiagramm wählt, sind nur Linienverläufe von einer Seite des Diagrammes zur anderen möglich, aber nicht wieder zurück.(→ Vergleich von y-Diagrammen und xy-Diagrammen ).
Schritte zur Erstellung eines einfachen y-Diagrammes.
- Datenbereich erstellen
- Datenbereich markieren
- Einfügen - Diagramm
- Bereich markieren, wo das Diagramm stehen soll (nur OpenOffice / StarOffice)
Die Reihenfolge der weiteren Einstellungen unterscheidet sich je nach verwendetem Programm. Achten Sie auf die folgenden Einstellungen:
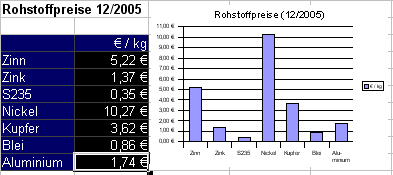
- Erste Zeile als Beschriftung: Ein
Die Zeilenüberschrift "€/kg" wird in die Legende übernommen. - Erste Spalte als Beschriftung: Ein
Die Namen der Metalle werden zur Beschriftung der x-Achse verwendet. - Diagrammtyp: Säulen, normal
Weitere Typen siehe unten - Datenreihen in: Spalten
Daten können auch in Zeilen angeordnet werden. Gewöhnlich erkennen die Tabellenkalkulationen die Anordnung selbstständig. - Diagrammtitel: Rohstoffpreise
- Achsentitel x-Achse und y-Achse: aus
Achsentitel sind Beschriftungen der x- und y-Achse, sie können nachträglich angebracht werden
7.1.1 Beispiele für y-Diagramme: ODS | XLS
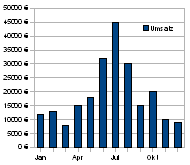
Säulendiagramm
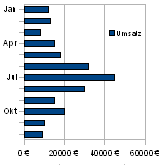
Balkendiagramm
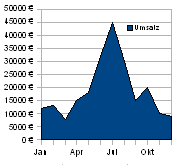
Flächendiagramm
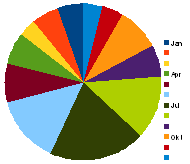
Kreisdiagramm
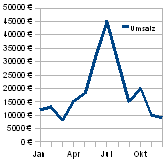
Liniendiagramm
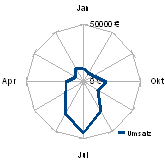
Netzdiagramm
⇑ ↑ 7.2 Einstellungen an Diagrammen ↓ ⇓
Der Feinschliff am Diagramm unterscheidet sich in den Details zwischen OO/SO bzw. MS. Bei MS-Excel ist es vor allem wichtig, wo ein Kontextmenü aufgerufen wird, denn es bietet abhängig vom Ort nur eine beschränkte Auswahl. Bei OpenCalc muss erst die richtige Stelle markiert sein, bevor das Kontextmenü aufgerufen wird. Einfacher ist es oft, das Menu zu verwenden. Nachdem ein Diagramm aktiviert wurde, passt sich das Menu nämlich an die Erfordernisse des Diagrammes an.
7.2.1 Diagramm-Assistenten wieder aufrufen
Auch für ein bestehendes Diagramm kann der Diagramm-Assistent aufgerufen werden, sodass alle Einstellungen geändert werden können. Man kann mit einem einfachen Diagramm beginnen und es nach und nach verbessern.
OpenOffice / StarOffice:
- Diagramm markieren mit Doppelklick → es bekommt einen breiten grauen Rahmen.
- Die einzelnen Einstellungen können danach auf zwei Wegen geändert werden:
- Kontextmenu (rechter Mausklick) auf dem element des Diagrammes, das geändert werden soll (Linie, Achse, Hintergrund, Titel..).
- Einfacher ist es, die Menuleiste zu nutzen, sich äußerlich kaum geändert hat, aber jetzt alle Auswahlmöglichkeiten für das Diagramm enthält.

MS-Excel:
- Diagramm markieren mit einfachem Klick auf das Diagramm
- Kontextmenu (rechter Mausklick) auf dem element des Diagrammes, das geändert werden soll (Linie, Achse, Hintergrund, Titel..).
7.2.2 Einstellmöglichkeiten
Wenn ein Diagramm aktiviert wurde, können alle Details des Diagrammes geändert werden. Im Folgenden sind die Menupunkte aufgezählt. Um sie kennenzulernen ist es das Beste, wenn Sie ausgiebig damit herumspielen.
- Format - Datenbereich
- legt fest, welche Daten dargestellt werden. Einstellungen im Beispiel:
- Datenreihe in Spalten
- Erste Zeile als Beschiftung: Ein
Wenn die Zellen "Drehmoment" und "Leistung" im Datenbereich eingebunden sind, werden die Texte für die Legende übernommen. Im Beispiel ist die Legende allerdings ausgeschaltet. - Erste Spalte als Beschriftung: Ein
Übernimmt die Zahlen oder Texte in der ersten Spalte für die Beschriftung der x-Achse. Hier sind es die Drehzahlwerte 0,500,1000 U/min.
- Format - Diagrammoptionen
- legt die Art des Diagrammes fest. (→ Beispiele für y-Diagramme )
- Einfügen - Titel / Format - Titel
- für die Titel "Verbrennungsmotor", "Drehmoment.." und "Drehzahl..".
- Einfügen - Gitter / Format - Gitter
- Im Beispiel ist das Gitter der x-Achse ausgeschaltet.
- Einfügen - Legende / Format - Legende
- Dient der Zuordnung der Kurven zu den Daten. Im Beispiel ist die Legende ausgeschaltet.
- Format - Diagrammfläche
- legt Farben, Umgrenzung usw. des ganzen Diagrammes fest. Einstellungen im Beispiel:
- Fläche - Füllung - Farbe: weiß
Wenn man keine Farbe wählt, scheint das Rautenmuster der Zellen durch das Diagramm durch.
- Fläche - Füllung - Farbe: weiß
- Format - Diagrammwand
- legt Farben, Umgrenzung usw. des Diagrammes zwischen x- und y-Achse fest. Einstellungen im Beispiel:
- Fläche - Füllung: keine
Mit den Vorgabeeinstellungen wird die Diagrammwand meistens grau dargestellt, aber das senkt den Kontrast des Diagrammes und erhöht Druckkosten.
- Fläche - Füllung: keine
- Kontextmenu auf einer Kurve im Diagramm - Objekteigenschaften
- Nach einem rechten Mausklick auf einer Kurve kann man unter Objekteigenschaften einstellen:
- Linie
Strichstärken, Farben und Linienarten der gewählten Linie. - Datenbeschriftung
Hier wird angegeben, womit die Linie beschriftet wird. Möglich sind die y-Datenwerte oder ein Beschriftungstext aus einer zusätzlichen Datenreihe. Die Beschriftung wird dort angezeigt, wo der Datenpunkt liegt. - Zeichen und Schrifteffekt
Formate der Beschriftung. - Statistik
Hier sind Einstellungen zum Näherungsverfahren für die Kurven möglich. - Optionen
Sind notwendig, wenn man eine Kurve an der sekundären y-Achse (rechte Skale) ausrichten möchte.
- Linie
- Format - Achsen
- Einstellungen im Beispiel für die linke y-Achse (schwarz):
- Schrifteffekt - Schriftfarbe: schwarz
- Beschriftung - Beschriftung anzeigen: Ein
- Skalierung - Maximum: 400
Drückt die schwarze Drehmomentkurve nach unten. - Skalierung - Hauptintervall: 50
Stellt an der Achse in 50er-Schritten dar. - Skalierung - Hilfsintervall: 5
Teilt die Hauptintervalle in 5 gleich große Hilfsintervalle, die im nächsten Punkt der Strichaufzählung durch kurze Linien markiert werden. - Skalierung - Haupt-/Hilfsintervall: Außen
- Die rechte y-Achse (blau) ruft man in zwei Schritten auf, wobei der erste Schritt entfallen kann:
- Einfügen - Achsen - Sekundäre Achsen - y-Achse: Ein
- Kontextmenu auf einer Kurve im Diagramm - Objekteigenschaften - Optionen - Datenreihe ausrichten an - Sekundäre y-Achse: Ein
- Einfügen - Achsen - Sekundäre Achsen - y-Achse: Ein
- Die Beschriftung der Achsen mit Zahlen und Einheiten ist auf zwei Wegen möglich: Entweder man formatiert die Datenreihen bereits mit Einheiten (→ Zahlenformate ) und übernimmt das "Quellenformat" in das Diagramm, oder man formatiert wie im Beispiel die Zahlen im Diagramm:
- Format - Achsen - y-Achse - Zahlen - Quellenformat: Aus - Format-Code: 0" Nm"
- Die x-Achse kann im Beispiel nicht skaliert werden, da es sich um ein y-Diagramm handelt. Wenn man die x-Achse skalieren möchte, muss man ein xy-Diagramm daraus machen. (→ xy-Diagramme )
⇑ ↑ 7.3 xy-Diagramme ↓ ⇓
Auf den ersten Blick bieten xy-Diagramme weniger Möglichkeiten als y-Diagramme, da sie nur Linien und Punkte darstellen können. Bei genauerer Betrachtung sind sie aber wesentlich vielseitiger, weil sie beliebige Linien zeichnen können. Damit ist - zumindestens theoretisch - jedes Diagramm möglich.
Ein xy-Diagramm zeichnet Linien oder Punkte nach Koordinaten. Dafür sind mindestens 2 Datenreihen für die x-y-Wertepaare nötig. Wertepaare stehen nebeneinander.
Wenn man mehrere Linienzüge in einem Diagramm darstellen möchte, verwendet man für die x-Werte nur eine einzige Spalte, während jede Kurve eine eigene Spalte für die y-Werte erhält.
Auch in xy-Diagrammen kann eine zusätzliche Datenreihe mit Zahlen oder Texten für die Beschriftung eingefügt werden. Diese Beschriftung wird aber nicht an der x-Achse angezeigt, sondern an der Position des zugehörigen Wertepaares im Diagramm. Die Zahlenwerte an den x- und y-Achsen wird aus den Werten gebildet, die sich aus den x-y-Wertepaaren ergeben.
Die x-Achse kann bei xy-Diagrammen skaliert werden, d.h. größter und kleinster Wert Wert der Skale, Skalenabstände usw. können manuell verändert werden.
Beispiel für ein xy-Diagramm

Datenbereich für das Phasendiagramm
Im Beispiel sind die folgenden Einstellungen gewählt
- Datenbereich B3: M8
Die Spalten A und N dienen nur der Erklärung und werden im Diagramm nicht benötigt. - Datenreihe in Zeilen
- Erste Zeile als Beschriftung: Ein
Dadurch können die hellblau unterlegten Texte in der obersten Zeile 3 als Beschriftung des Diagrammes verwendet werden. Wie das geht, steht etwas weiter unten. - Die nächste Zeile, in diesem Fall Zeile 4 zwischen Al und Si, wird automatisch als Datenreihe für die x-Werte interpretiert. Alle Linien verwenden dieselbe x-Datenreihe. x-Werte dürfen mehrfach und in jeder beliebigen Reihenfolge vorkommen. Die Reihenfolge der x-y-Werte bestimmt den Verlauf einer Linie.
- Die folgenden 4 Zeilen enthalten 4 y-Datenreihen für 4 Linienzüge.
- Linie 1 (Liquiduslinie) verläuft von (0%; 660°C) über (12%; 577°C) bis zu (30%; 750°C). Die Linie wird nicht vollständig dargestellt, weil das Maximum der x-Achse auf 0,2 skaliert wurde. Das Phasendiagramm wird also nur bis 20% Siliziumanteil dargestellt.
- Linie 2 (Soliduslinie) verläuft von (0%; 577°C) bis zu (30%; 577°C) und ist auch nicht vollständig dargestellt.
- Linie 3 in Zeile 7 dient dazu, Beschriftung ins Diagramm zu bringen. Die Linie selbst ist in ihren Objekteigenschaften unsichtbar und mit Anzeige der Beschriftung eingestellt. Mit dieser Konstruktion kann man in einem Diagramm an jeder beliebigen Stelle Text unterbringen. Im Beispiel steht der Text "Schmelze" über der "Koordinate" (10%; 650°C).
- Linie 4 (Eutektikum) verläuft senkrecht von (12%; 577°C) bis (12%; 0°C). Auch sie wird nicht vollständig dargestellt, weil die y-Achsen mit dem Minimum 550°C skaliert sind.
- Erste Spalte als Beschriftung: Aus
Im Beispiel haben die Spalten A und N keine Funktion für das Diagramm. - Die Beschriftung der x-Achse wird automatisch aus dem Datenbereich der x-Werte gebildet. Dabei kann die Skalierung der x-Achse (von.. bis in… -Schritten) bei xy-Diagrammen manipuliert werden (→ Achsen skalieren . Bei y-Diagrammen ist das nicht möglich.
⇑ ↑ 7.4 y-Diagramm und xy-Diagramm im Vergleich ↓ ⇓
y-Diagramme für (eindeutige) Funktionen
xy-Diagramme für Relationen (mehrdeutige Funktionen)
Typischer Vertreter eines y-Diagrammes ist das Balkendiagramm, das eine Reihe von Zahlen grafisch darstellt. Die Abstände zwischen den Balken sind gleichmäßig.
Ein xy-Diagramm zeichnet Punkte oder Linien im Diagramm nach Koordinaten. Damit sind - theoretisch - beliebige Linienverläufe möglich.
Für ein y-Diagramm benötigt man in einer Tabellenkalkulation nur eine(! ) Datenreihe, und zwar für die y-Werte, die mit gleichmäßigen Abständen dargestellt werden.
Wenn die Daten als Liniendiagramm dargestellt werden, ist das Liniendiagramm äußerlich leicht mit einem xy-Diagramm zu verwechseln. Tatsächlich sind aber nur Kurvenverläufe von einer Seite des Diagrammes zur anderen ohne Umkehr möglich (Funktionen).
Für ein xy-Diagramm benötigt man in einer Tabellenkalkulation mindestens 2 Datenreihen, die als x-y-Wertepaare (Koordinaten) interpretiert werden.
Mit xy-Diagrammen sind beliebige Linienverläufe möglich (Relationen).
y-Diagramme können je nach Version der Tabellenkalkulation als Liniendiagramm, Säulendiagramm, Balkendiagramm, Kreisdiagramm (Tortendiagramm, Kuchendiagramm), Flächendiagramm, Netzdiagramm usw. dargestellt werden. Dabei variieren die Details, aber das oben genannte Prinzip bleibt erhalten.
xy-Diagramme werden als Linien oder Punkte dargestellt.
Es sind mehrere Kurven in einem Diagramm möglich. Jede Kurve benötigt eine eigene Datenreihe für ihre y-Werte. Wenn zwei y-Daten nebeneinander stehen, werden sie denselben x-Werten zugeordnet.
Wenn man mehrere Linienzüge in einem Diagramm darstellen möchte, verwendet man für jede Kurve eine eigene Spalte mit y-Werten. Die x-Werte stehen für alle Koordinaten in einer einzigen Spalte.
Wenn in einer zusätzlichen Reihe Zahlen oder Texte für die x-Achse angegeben sind, dienen diese nur der Beschriftung, ändern aber nicht den Linienverlauf. Die y-Achse wird mit den Zahlenwerten beschriftet, die sich aus den y-Werten ergeben.
Auch in xy-Diagrammen kann eine zusätzliche Datenreihe mit Zahlen oder Texten für die Beschriftung eingefügt werden. Diese Beschriftung wird aber nicht an der x-Achse angezeigt, sondern an der Position des zugehörigen Wertepaares im Diagramm. Die Zahlenwerte an den x- und y-Achsen wird aus den Werten gebildet, die sich aus den x-y-Wertepaaren ergeben.
Die x-Achse kann bei y-Diagrammen nicht händisch skaliert werden.
Die x-Achse kann bei xy-Diagrammen manuell skaliert werden. Einstellbar sind größter und kleinster Wert Wert der Skale, Skalenabstände, Intervallmarkierungen usw.
Formelmäßig werden y-Diagramme mit Funktionen bzw. eindeutigen Funktionen beschrieben. In eindeutigen Funktionen gibt es für jeden x-Wert nicht mehr als einen y-Wert. Ihre Kurve verläuft in einem Diagramm von einer Seite zur anderen, kann aber niemals umkehren.
Formelmäßig werden xy-Diagramme mit Relationen bzw. mehrdeutigen Funktionen beschrieben. In Relationen kann es für jeden x-Wert mehrere y-Werte geben und ihre Kurve kann beliebig im Diagramm verlaufen.
⇑ ↑ 7.5 Weitere Beispiele ↓ ⇓
Übung " Normalverteilung "
Aufgabe: Erstellen Sie ein Arbeitsblatt zur Auswertung Normalverteilter Messreihen.
Arbeitsblatt: PDF mit ausführlicher Arbeitsanleitung
Musterlösung: PDF, OpenOffice2, Excel97 .
Übung " Operationscharakteristiken von AQL-Anweisungen "
Aufgabe: Erstellen Sie eine Grafik zur Darstellung von Operationscharakteristiken von AQL-Anweisungen.
Arbeitsblatt: PDF mit ausführlicher Arbeitsanleitung
Musterlösung: PDF, OpenOffice1, Excel97 .
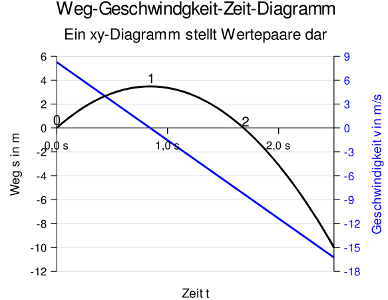
Ein Geschwindigkeits-Zeit-Diagramm als xy-Diagramm.
Im Beispiel ist es auch als y-Diagramm ausgeführt.
Download: ODS | XLS | PDF
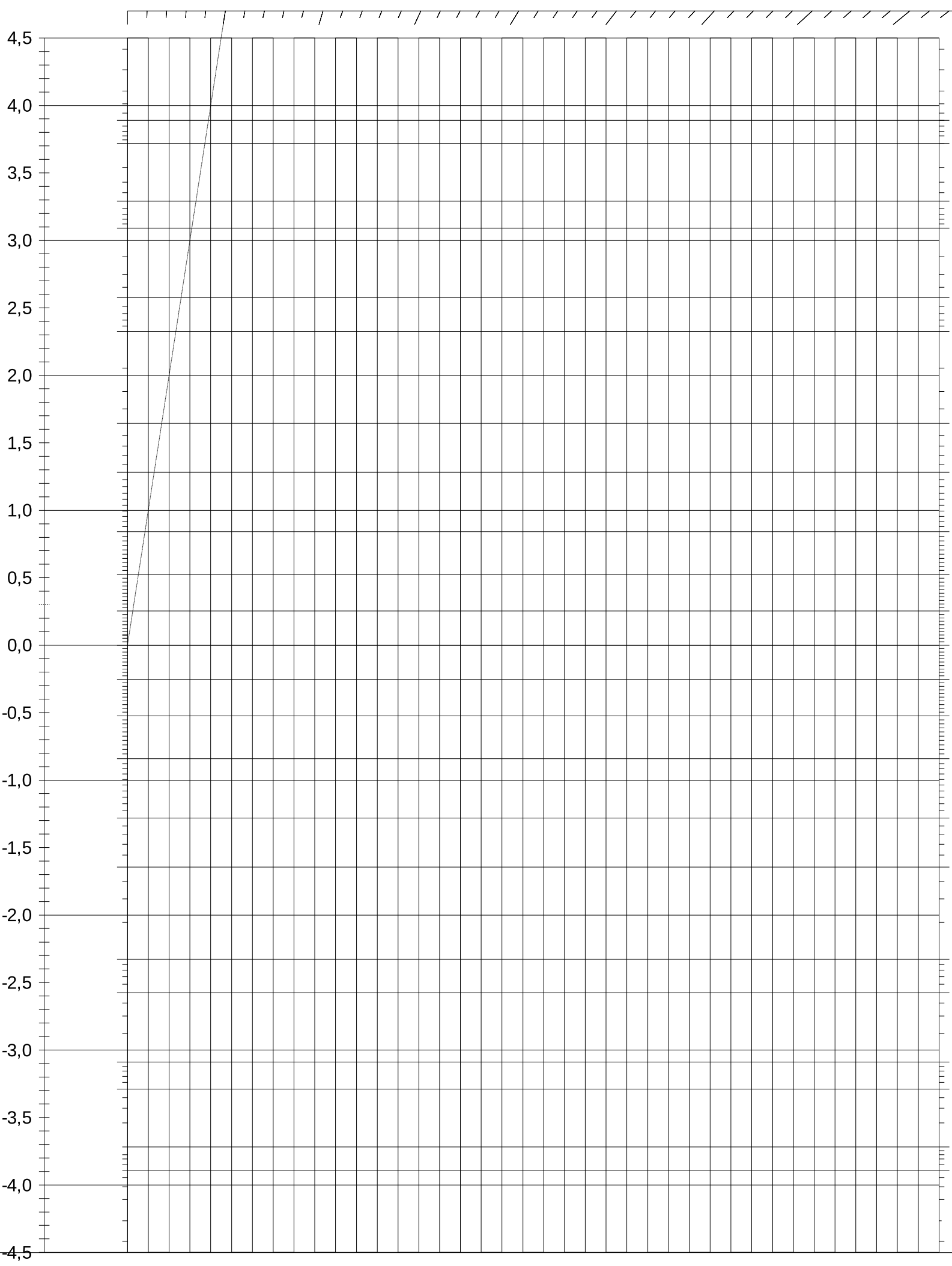
Wahrscheinlichkeitsnetz für Normalverteilte Messreihen:
Download: ODS (LibreOffice Calc)
Download: ODG (LibreOffice Draw, zum Nachbearbeiten der Linienarten usw.)
Download: ODS (LibreOffice Text)
Download: PDF (PDF aus der Textversion)
⇑ ↑ 7.6 Probleme ↓ ⇓
So viel ich sonst von OpenOffice halte, aber bei Diagrammen hat es noch Nachholbedarf. Die Bedienung hat sich in den letzten Versionen zwar deutlich vereinfacht, sodass die Diagramme jetzt relativ komfortabel erstellt werden können, aber sensibel sind Diagramme immer noch. (2008).
Mein Problem ist, dass ich komplexe Diagramme erstellt habe und sie kopieren möchte, um Varianten von ihnen zu erzeugen. Da muckt OpenOffice bis hin zu reproduzierbaren Abstürzen. Unter Beachtung der folgenden Regeln hat es dann doch noch geklappt:
- Wenn man ein Diagramm innerhalb eines Tabellenblattes kopiert, bezieht sich die Kopie immer auf den ursprünglichen Datenbereich. Die Änderung des Datenbereiches kann ganz schön umständlich sein, wenn das Diagramm nicht sehr einfach ist.
- Wenn man ein Tabellenblatt mit einem Diagramm per "Tabelle verschieben/kopieren" innerhalb derselben Datei kopieren möchte, gilt das gleiche. Das kopierte Diagramm greift auf die ursprünglichen Daten im ursprünglichen Tabellenblatt zurück.
- Man muss das Tabellenblatt mit dem Diagramm in eine andere Datei kopieren, um eine wirkliche Kopie zu erhalten, die sich auch auf die Kopie der Daten bezieht. Wählen Sie dazu "Tabelle verschieben/kopieren - Ins Dokument". Leider treten dann immer noch genügend Probleme auf:
-
- Da ich es erlebt habe, dass beim Kopieren auch das ursprüngliche Diagramm vermurkst wurde, kopiere ich nur noch aus einer Kopie der Datei. Um weitere Probleme zu beseitigen, lösche ich auch alle anderen Tabellenblätter aus dieser Datei, bis nur noch das Tabellenblatt mit dem zu kopierenden Diagramm vorhanden ist.
- Vor dem Kopieren in eine andere Datei benenne ich das Tabellenblatt schon so um, wie es in der anderen Datei heißen soll. Umbenennen von Tabellenblättern mit Diagrammen führt nämlich gelegentlich zu Problemen, insbesondere wenn man dabei Fehler macht. In Dateien mit nur einem Tabellenblatt traten diese Probleme bei mir nicht auf.
- Noch eines seltsame Macke: Das Tabellenblatt mit dem Diagramm muss in der Zieldatei unbedingt ans Ende der Tabellen gestellt werden, sonst macht OO Probleme bei den Diagrammen. Tückischerweise sieht man diese Probleme nicht sofort, sondern erst, wenn man versucht, das kopierte Diagramm zu formatieren.
- Am sichersten ist es, die Varianten des Diagrammes in jeweils eigenen Dateien zu erstellen und dann nach und nach in eine neu angelegte Datei zu kopieren.
Das ist alles ziemlich lästig, aber kein Grund, bei MS zu bleiben. Das hat auch genügend Macken, eben andere. Und bei OO bleibt immer noch die Hoffnung auf die nächste Version.
⇑ ↑ 8 Zusammenspiel von Text und Zahlen ↓ ⇓
Tabellenkalkulationen unterscheiden Text und Zahlen ( → Zelleninhalte ) und reagieren auch unterschiedlich auf sie. In diesem Kapitel geht es darum, einige Grenzübergänge zwischen Text und Zahlen zu zeigen.
⇑ ↑ 8.1 Text und Zahl in einer Zelle ↓ ⇓
Man kann Zahlen in Texte umwandeln und danach wie Texte behandeln. Damit können beliebige Texte und Zahlen in einer Zelle dargestellt werden.
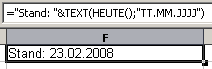
Text und aktuelles Datum in einer Zelle
- HEUTE() setzt das aktuelle Datum ein
- TEXT(Zahl; Format) wandelt das Datum in einen Text um
- "TT.MM.JJJJ" legt fest, in welchem Format das Datum angegeben wird ( → Datum und Zeit )
- "Stand: " Zeichen zwischen Anführungszeichen werden immer als Text interpretiert
- & verbindet zwei Texte.
⇑ ↑ 8.2 Zahlen mit Maßeinheiten ↓ ⇓
Für Ingenieure und Naturwissenschaftler gehören Zahl und Einheit selbstverständlich zusammen, aber Tabellenkalkulationen tun sich damit noch schwer. Wenn man mit Einheiten rechnen muss, ist die einfachste Lösung immer noch, die Einheiten als Texte in getrennten Zellen zu verwalten. Wenn sich die Einheiten beim Rechnen nicht ändern, z.B. Währungen, kann man sie auch durch Formatierung darstellen.
Neuere Versionen bieten Funktionen, mit denen Zahlen für andere Einheiten umgerechnet werden können.
- =UMWANDELN_ADD(100;"cm";"in")
Ergebnis: 39,37
bedeutet: 100 cm = 39,97 inch - Mögliche Maßeinheiten sind
- Masse: g, sg, lbm, u, ozm, stone, ton, grain, pweight, hweight, shweight
- Länge: m, mi, Nmi, in, ft, yd, ang, Pica, ell, parsec
- Zeit: yr, day, hr, mn, sec
- Druck: Pa, atm, mmHg, Torr, psi
- Kraft: N, dyn, pond
- Energie: J, e, c, cal, eV, HPh, Wh, BTU
- Leistung: W, HP, PS
- Feldstärke: T, ga
- Temperatur: C, F, K, Reau, Rank
- Volumen: l, tsp, tbs, oz, cup, pt, qt, gal, m3, mi3, Nmi3, in3, ft3, yd3, ang3, Pica3, barrel, bushel, regton, Schooner, Middy, Glass
- Fläche: m2, mi2, Nmi2, in2, ft2, yd2, ang2, Pica2, Morgen, ar, acre, ha
- Geschwindigkeit: m/s, m/h, mph, kn, admkn
- Mögliche Präfixe für die Größenordnung
- verkleinernd: d, c, m, u, n, p, f, a, z, y
- vergrößernd: e, h, k, M, G, T, P, E, Z, Y
Einheit umrechnen
Zahlenformate verändern nur die Darstellung der Zahl, nicht ihren Wert. Bei Währungen spielt das keine Rolle, weil sich diese bei Berechnungen nicht ändern. Oder verwendet jemand die Einheit €²? ;-)
Einheit per Formatierung
Übung " Kalender "
Aufgabe: Erstellen Sie einen Kalender.
Arbeitsblatt: PDF mit ausführlicher Arbeitsanleitung
Musterlösung: PDF, OpenOffice1 .
⇑ ↑ 9 GrafischeElemente ↓ ⇓
⇑ ↑ 10 Formatvorlagen ↓ ⇓
Beim Formatieren unterscheidet man harte und weiche Formatierung. Ein Beispiel für harte Formatierung ist, wenn man jede Überschrift einzeln fett formatiert. Weiche Formatierung ist, wenn man jeder Überschrift eine Formatvorlage zuweist und in der Formatvorlage das Format fett angibt. Beide Überschriften sehen gleich aus, aber der Unterschied wird deutlich, wenn man alle Überschriften von fett auf kursiv ändern will. Harte Formatierungen müssen einzeln geändert werden, bei weichen Formatierungen genügt es, die Formatvorlage zu ändern (→ Formatvorlagen ).
Weiche Formatierungen funktionieren so ähnlich wie Layer oder Stilvorlagen in CAD-Programmen undCSS-Vorlagen in HTML-Texten. Formatvorlagen gibt es auch in Textverarbeitungsprogrammen wie StarWord, OpenOffice oder MS-Word.
Es gehört zu einem guten Programmierstil, Inhalt und Form zu trennen. Dies kann mit Formatvorlagen erreicht werden, da sie die Formatierung außerhalb des eigentlichen Textes festlegen. Der erste Nutznießer eines solchen Programmierstiles ist der Programmierer selbst, denn er erleichtert sich damit die Pflege seiner Seiten. Weitere Nutznießer sind z.B. Sehbehinderte, die sich den Text von speziellen Programmen vorlesen lassen. Sie müssen nämlich nicht wissen, welche Farbe und Größe ein Text hat, sondern ob es sich um eine Überschrift, einen Normaltext, ein Zitat, eine Hervorhebung o.ä. handelt. Diese Information kann man in Formatvorlagen finden.
⇑ ↑ 11 Bedingte Formate ↓ ⇓
⇑ ↑ 12 Datenbankfunktion ↓ ⇓
= INDEX (..)
= SVERWEIS(..)
3D-Matrix
⇑ ↑ 13 Zirkelschluss - Berechnung von Gleichungssystemen ↓ ⇓
⇑ ↑ 14 Daten sortieren und auswählen ↓ ⇓
⇑ ↑ 14.1 manuelles Sortieren ↓ ⇓

Namensliste zum Sortieren markieren
Oft genug müssen Noten in andere Listen übertragen werden. Da ist es tückisch, wenn eine Liste nicht exakt alphabetisch sortiert ist.
Sortieren Sie Listen immer automatisch, um Fehler zu vermeiden.
- Markieren Sie die ganzen Zeilen, die sortiert werden sollen, indem Sie mit gedrückter linker Maustaste über die Zeilennummern fahren.
- Wählen Sie in der Menüleiste Daten - Sortieren.. - Sortierkriterien - Sortieren nach: Spalte B - OK
Aufpassen: Im Duden wird Händel zwischen Handel und handelbar sortiert, und nicht bei Haendel. Viele Programme, auch ältere Tabellenkalkulationen oder neuere Schulverwaltungsprogramme, machen das falsch, und wer da nicht aufpasst, hat leicht die Noten falsch übertragen.
Tipp: Gewöhnen Sie sich an, vor dem Sortieren immer ganze Zeilen zu markieren, indem Sie mit der Maus über die Zeilennummern fahren. Wenn Sie dies nicht tun und einmal eine Spalte vergessen, wird diese nicht mitsortiert, und Sie werden merken, dass die richtigen Noten bei den falschen Schülern ärgerlich sind.
⇑ ↑ 14.2 Datensatz manuell per Dropdownliste auswählen ↓ ⇓

Werkstoff aus einer Tabelle per Listenfeld wählen
zugehörige Zugfestigkeit mit =SVERWEIS() herausziehen
Wer häufig mit tabellierten Werten arbeitet, liegt bei einer Tabellenkalkulationen natürlich richtig. Dort müssen die Datensätze nicht händisch abgetippt werden, sondern können per Listenfeld ausgewählt werden. Die benötigten Tabellenwerte können zB. mit dem Befehl =SVERWEIS() aus der Tabelle entnommen werden.
Im Bild rechts wird der Werkstoff S235JR per Listenfeld ausgewählt und die zugehörige Zugfestigkeit per =SVERWEIS() automatisch ergänzt.
Listenfeld einfügen
OpenOffice
- Markieren Sie eine Zelle, hier A3
- Daten - Gültigkeit - Kriterien -
- Zulassen: Zellbereich
- Quelle: C3: C6
- Daten - Gültigkeit - Eingabehilfe
Hier können Sie Hinweise eingeben, die erscheinen, wenn man mit der Maus über das Listenfeld fährt.
MS-Excel
- Markieren Sie eine Zelle, hier A3
- Daten - Gültigkeit - Einstellungen / Gültigkeitskriterien
- Zulassen: Liste
- Quelle: C3: C6
- Daten - Gültigkeit - Eingabemeldung
Hier können Sie Hinweise eingeben, die erscheinen, wenn man mit der Maus über das Listenfeld fährt.
Bei beiden Programmen passt sich die Quellenangabe des Listenfeldes nicht an, wenn die Werkstofftabelle später durch Einfügen von Zeilen erweitert wird. Das ist lästig, weil das Hinzufügen von Zeilen oder Spalten sonst ein bequemes Mittel ist, Tabellen zu erweitern ohne sich um die Formeln mit Adressbereichen kümmern zu müssen.
Man kann das Problem umgehen, indem man dem Bereich einen Namen gibt und den Bereichsnamen verwendet.
Zugehörigen Tabellenwert mit =SVERWEIS() aus der Tabelle entnehmen ("Zugfestigkeit 340")
B3: =SVERWEIS(A3;C3: F6;3;0)
- A3: entnimmt den gewählten Wert S235JR aus dem Listenfeld und sucht ihn in der ersten Spalte der Tabelle C3: F6
- C3: F6: enthält die Werkstofftabelle
- 3: entnimmt den Zellinhalt aus der dritten Spalte der Tabelle (und der Zeile, in der S235JR steht). Im Bild ist es die Zelle E4 mit dem Wert 340.
- 0: bedeutet, dass die Werkstofftabelle nicht alphabetisch sortiert ist.
Tipp : Hinterlegen Sie Tabellen farblich, damit Sie wissen, wo sie anfangen und aufhören. Verwenden Sie auch nur Formeln mit Adressbereichen, zB = SUMME(C1: C3) statt =C1+C2+C3, denn die Adressbereiche passen sich an, wenn Sie die Tabellen durch Einfügen von Zeilen oder Spalten erweitern.
Tabellenblatt " Listenfeld "
Im Bild oben sehen Sie eine Werkstofftabelle. Aus der Werkstofftabelle soll mittels eines Listenfeldes ein Werkstoff ausgewählt werden. Für den gewählten Werkstoff soll die Zugfestigkeit angezeigt werden. Natürlich könnte man mit der Zugfestigekit auch weitere Berchnungen durchführen.
Musterlösung: LibreOffice, Excel97 .
⇑ ↑ 14.3 Werte aus Tabellen herausziehen ↓ ⇓
Übung " Matrixfunktionen "
Häufig ist es nötig, Werte aus einer Tabelle herauszuziehen, z.B. die Preise für eine Artikelnummer, die Zugfestigkeit für einen Werkstoff oder den Flankendurchmesser für eine bestimmte Gewindegröße.
Im Übungsblatt wird die Aufgabe gestellt, dass nach Eingabe einer Postleitzahl in den Nachbarzellen Ortsname und Vorwahl automatisch übernommen werden.
Zur Lösung werden zwei Verfahren angeboten. Das erste Verfahren mit =VERGLEICH(), =ADRESSE() und =INDIREKT() ist kompliziert, aber vielseitig. Das zweite Verfahren mit =SVERWEIS() bzw. =WVERWEIS() ist einfacher und für die meisten Anwendungsfälle völlig ausreichend.
Arbeitsblatt: PDF mit ausführlicher Arbeitsanleitung
Musterlösung: OpenOffice2, Excel97 .
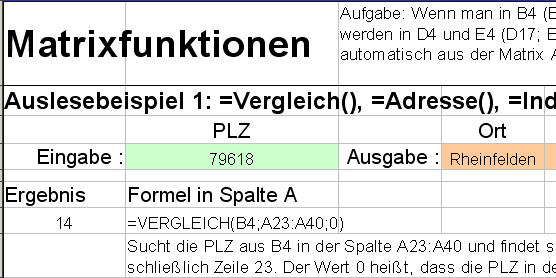
⇑ ↑ 14.4 Tabelle automatisch nach Punkten sortieren ↓ ⇓
Übung " Turnierplan mit Tabelle "
Sie wollen eine Tabelle sortiert in eine andere Tabelle übertragen, zB. eine Sporttabelle erstellen?
Im Tabellenblatt finden Sie ein Beispiel dafür.
Die Sortierung erfolgt mit der Funktion =RANG(), die sortierte Übertragung mit der FUNKTION =SVERWEIS().
Musterlösung mit kurzer Beschreibung: LibreOffice, Excel97 .
⇑ ↑ 14.5 Nur bestimmte Zellen zählen oder summieren ↓ ⇓
Wie hoch sind die Umsätzen insgesamt an Montagen? Wie oft kommt das Wort "Bleistift" in einer Liste vor? Diese Fragen beantworten die die Befehle =SUMMEWENN(..) und =ZÄHLENWENN(..), ohne dass man Montag oder Bleistift mit =WENN(..) aussortiert. Beispiele: ODS / XLT
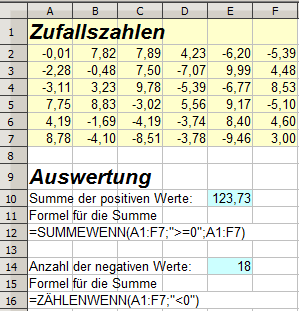
Im Bild rechts wird eine Reihe von Zufallszahlen generiert. Es soll ermittelt werden, wie groß der Anzahl der negativen Zahlen und wie groß die Summe der positiven Zahlen ist.
=ZÄHLENWENN(A1: F12;"<0")
zählt im Bereich A1: F12 die Anzahl derjenigen Zellen, deren Inhalt kleiner als 0 ist.
- Das Suchkriterium muss als Text geschrieben werden, deshalb steht es in Anführungszeichen.
- Wenn das Suchkriterium nicht feststeht, kann man es auch aus anderen Zellen holen.
Beispiel: =ZÄHLENWENN(A1: F12;"<"&G1)
zählt alle Zellen, deren Inhalt kleiner ist als der Inhalt der Zelle G1.
Beachten Sie den Textoperator & (kaufmännisches UND), der "<" mit G1 als Text verbindet. - Weitere Beispiele finden Sie in der Hilfefunktion von Openoffice unter dem Stichwort "Zählenwenn".
=SUMMEWENN(A1: F7;">=0";A1: F7)
summiert diejenigen Zufallszahlen, die größer oder gleich 0 sind.
- Das Suchkriterium "=2" muss als Text geschrieben werden, deshalb steht es in Anführungszeichen.
- Wenn im Bereich B3: I3 das Suchkriterium "=2" zutrifft, wird der in B4: I4 korrespondierende Inhalt zur Summe hinzugefügt.
- Libreoffice nummeriert die Wochentage ab dem Sonntag, also steht 2 für einen Montag.
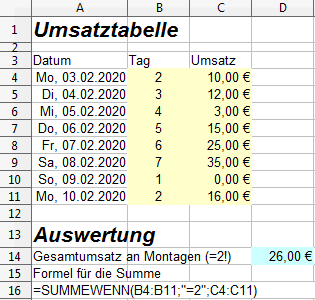
=SUMMEWENN(B3: I3;"=2";B4: I4)
summiert diejenigen Umsätze in der Umsatztabelle, über denen eine "2" steht.
- Das Suchkriterium "=2" muss als Text geschrieben werden, deshalb steht es in Anführungszeichen.
- Wenn im Bereich B3: I3 das Suchkriterium "=2" zutrifft, wird der in B4: I4 korrespondierende Inhalt zur Summe hinzugefügt.
- Libreoffice nummeriert die Wochentage ab dem Sonntag, also steht 2 für einen Montag.
⇑ ↑ 14.6 Matrix / Matrizen transponieren (Zeilen und Spalten vertauschen) ↓ ⇓
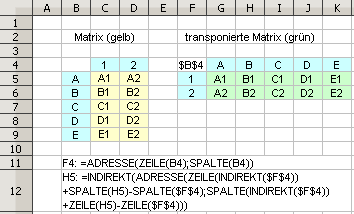
Die Befehle =INDIREKT() und =ADRESSE kann man auch verwenden, um eine Matrix zu transponieren, d.h. ihre Zeilen und Spalten zu vertauschen.
Im Bild rechts steht die ursprüngliche Matrix gelb hinterlegt im Adressbereich C5: D9. Rechts daneben steht die transponierte Matrix grün hinterlegt im Adressbereich G5: K6. Die blauen Bereiche dienen der Bezeichnung von Zeilen und Spalten und gehören streng genommen nicht zu den Matrizen, wurden aber genauso transponiert.
- Wo die ursprüngliche Matrix (gelb) liegt, wird links oben von der transponierten Matrix (grün) im Feld F4 durch die Adresse B4 (links oben von der ursprünglichen Matrix) definiert. Man kann die Adresse B4 oder $B$4 manuell Hand eingeben, oder mit einer Formel wie hier
F4: =ADRESSE(ZEILE(B4);SPALTE(B4)) - Die Zellen werden mit einer kopierfähigen Formel transponiert, hier das Beispiel aus der Zelle H5 der Tabellenkalkulation (bzw. B1 der grünen Matrix):
H5: =INDIREKT(ADRESSE(ZEILE(INDIREKT($F$4))+SPALTE(H5)-SPALTE($F$4);SPALTE(INDIREKT($F$4))+ZEILE(H5)-ZEILE($F$4)))
Die Zelle H5 muss nur noch in den gewünschten Bereich kopiert werden. - Beispiel: ODS / XLS
Hinweis: Wenn Sie die Musterlösung per Kopieren und Einfügen übertragen, müssen Sie die Adressen $F$4 innerhalb einer Formel anpassen und diese dann kopieren.
⇑ ↑ Anhang A: Fehlermeldungen in den Zellen ↓ ⇓
| Fehlermeldungen | OpenOffice / StarOffice | MS Excel |
|---|---|---|
| Spalte zu schmal | ######### | |
| Division durch 0 | Err: 503 | #DIV/0! |
| Eingabe liegt nicht im sinnvollen Bereich (z.B. Wurzel aus einer negativen Zahl) | Err: 502 | #ZAHL! |
| Eingabe hat den falschen Typ (z.B. Multiplikation mit einem Text) | #Wert? | |
| Unbekannte Funktion (z.B. durch Tippfehler) | #name? | |
| Fehler in der Funktion (z.B. zu wenige Argumente: =wenn(a1<0;"Wert ist kleiner als Null"); es fehlt die Angabe für Wert größer/gleich Null) | #NV | #NV |
In StarOffice findet man die vollständige Liste der Fehlercodes (Err: ..) unter dem Stichwort "Err" in Hilfe - index. Wenn der rote Punkt in der Symbolleiste der Hilfe gedrückt ist, bleibt der aktuelle Hilfetext erhalten, ansonsten versucht die Hilfe mit Ihren Eingaben Schritt zu halten.
In Excel findet man die Fehlercodes unter dem Stichwort der Fehlermeldung, z.B. "#Null! " ebenfalls in Hilfe - index
Weitere Fehler: Verschwunden ( Leiste, Zahl )
⇑ ↑ Anhang B: Arbeitstechniken ↓ ⇓
Zur effizienten Erstellung und Bearbeitung größerer Tabellenblätter sollte man die verschiedenen zeitsparenden Techniken kennen. Soweit die Techniken im vorherigen Kapiteln schon beschrieben wurden, sind sie hier nur noch verlinkt.
- Zellen kopieren
- Zellen verschieben
- Formeln eingeben siehe Kapitel Eingabe von Formeln
- Zeilen und Spalten einfügen
⇑ ↑ B.1 noch leer ↓ ⇓
⇑ ↑ B.2 Zellen verschieben ↓ ⇓
Kopieren in angrenzende Bereiche
Will man Zellen in angrenzende Zeilen oder Spalten kopieren, kann man sie am kleinen Rechteck, das rechts unten am markierten Bereich liegt, greifen und ziehen. Wenn in den Zellen nur Texte oder Zahlen stehen, werden diese manchmal fortgeführt.
Übung "Kopieren" ( Lösungen im Downloadbereich ). Aufgabe: Schreiben Sie eine 1 in Zelle A1, ein "A" in Zelle B1, und "Mo" in Zelle C1, und kopieren Sie die 3 Zellen nach unten: Die Zelle A1 wird kopiert in 1,2 3,4..; Die Zelle B1 wird kopiert in Mo, Di, Mi, Do; die Zelle C1 bleibt unverändert in A; A; A..
Die Sortierlisten (das automatische Zählen) kann angepasst werden, man kann sogar eigene Sortierlisten erzeugen in:
- Excel: Extras - Optionen - AutoAusfüllen
- StarOffice: Extras - Optionen - Tabellendokument - Sortierliste
Wo man das automatische Zählen ausschalten kann, weiß ich nicht, aber ich behelfe mir mit der folgenden Kopiertechnik.
Kopieren in nicht angrenzende Bereiche (in Zwischenspeicher kopieren, neuen Bereich markieren, einfügen)
Kopieren klappt auch mit mehreren Zellen gleichzeitig.
Übung: erstellen Sie eine Matrix mit 2x3 zellen, schreiben sie nebeneinander 1,3, 5 und darunter a, b, c. Kopieren Sie die Matrix nach unten, nach rechts und in nicht angrenzende Bereiche. Beobachten Sie das Verhalten.
⇑ ↑ B.3 Zellen und Spalten einfügen ↓ ⇓

Wenn man ein Tabellenblatt zum Auswerten von Daten anlegt, sollte man den Datenbereich farblich markieren. So vermeidet man, versehentlich Daten in einen Bereich zu schreiben, der nicht ausgewertet wird. Den Datenbereich kann man nachträglich erweitern, indem man zwischendrin Zeilen oder Spalten ergänzt; Formeln, die Zellbereiche auswerten, passen sich dabei automatisch an, z.B. =SUMMEWENN(..) im Bild.
In LibreOffice 5.0 muss man bei der Erweiterung des Datenbereiches allerdings aufpassen: Diagramme erweitern ihren Datenbereich nicht, wenn man Zeilen einfügen, mit Spalten dagegen funktioniert es! ?
⇑ ↑ C Umfangreiche Tabellen anlegen ↓ ⇓
⇑ ↑ C.1 Aufteilung des Blattes ↓ ⇓
Wenn man den Bescheid vom Finanzamt oder die Rechnung von der Versicherung geöffnet hat, geht der erste Blick auf das Blatt nach rechts unten, weil dort das Wichtigste steht: Der Betrag der Erstattung bzw. der Forderung.
An diese Blattaufteilung hat man sich so gewöhnt, dass man nicht mehr darüber nachdenkt. Sie ist aber keine natürliche Aufteilung, sondern eine Folge der mitteleuropäischen Buchführungstechniken. Seit Erfindung derselben durch italienische Bankiers schreibt man links die Erläuterung und rechts die Beträge. Die Summe der Beträge schreibt man rechts darunter, weil das besonders günstig für das Addieren von Hand ist.
Auf einzelnen (Papier-)Blättern ist diese Anordung sowohl praktisch als auch übersichtlich, und so haben wir uns jahrhundertelang daran gewöhnt.
Aber ein Tabellenblatt kann bis 65536 Zeilen enthalten, und wenn man dort das Ergebnis rechts unten sucht, muss man eine meterlange Buchrolle abwickeln (Die Älteren erinnern sich: -). Außerdem addiert die Tabellenkalkulation nicht mehr nach Adam Riese, sondern mit AMD oder Intel, und es ist ihr gleichgültig, wohin sie das Ergebnis schreiben soll.
Diese Erkenntnisse sollten Sie in die Gestaltung Ihres Tabellenblattes einfließen lassen:
Die wichtigsten Felder müssen leicht erreichbar sein.
Wichtig sind die Eingabefelder und die Ausgabefelder, d.h. die Ergebnisse. Unter Umständen gehören auch Diagramme dazu. Ideal ist es, wenn sie direkt auf einem Bildschirm sichtbar sind. Wenn dies nicht möglich ist, muss man die allerwichtigsten Ergebnisse auswählen und sofort sichtbar präsentieren.
Werkstofftabellen, Nebenrechnungen, lange Datenreihen usw. kann man aus dem Sichtbereich verbannen. Gut geeignet sind dazu weitere Tabellenblätter in einer Mappe, die aber benamst sein müssen, damit man sie im Bedarfsfall leicht findet.
⇑ ↑ C.2 komplizierte Formeln aufbauen ↓ ⇓
Theoretisch kann man meterlange Formeln direkt in die Formeleingabe-Leiste eintippen, aber je komplizierter die Formel wird, desto mehr Fehler macht man und desto unübersichtlicher wird die Fehlersuche - wenn man den Fehler überhaupt bemerkt. Es gibt für jeden Programmierer eine individuelle Grenze, ab der er mit systematischer Vorgehensweise Zeit spart gegenüber dem schnellen Eintippen (und der folgenden Fehlersuche). Ich empfehle im Zweifelsfalle lieber etwas mehr systematisches Vorgehen.
Als Beispiel dient eine Formel aus der Übung "Matrixfunktionen" bei Übungsbeispiele
=INDIREKT(ADRESSE(22+VERGLEICH(B4;$A$23: $A$40;0);2;1))
Die ganze Formel ist aus mehreren einzelnen Formeln verschachtelt und für den Ungeübten schon ziemlich unübersichtlich. Zur Entwicklung einer solchen Formel empfehle ich die folgende Vorgehensweise:
- Erproben Sie die Formeln an einfachen Beispielen, deren Ergebnis sie kennen.
- Bauen Sie die Formel schrittweise von innen nach außen in getrennten Zellen auf und testen Sie jeden Zwischenschritt gründlich. Beispiel:
-
- B6: =VERGLEICH(B4;$A$23: $A$40;0)
(in Zelle B6 steht die Formel… - B7: =ADRESSE(22+B6;2;1)
- B8: =INDIREKT(B7)
- B6: =VERGLEICH(B4;$A$23: $A$40;0)
- Wenn die einzelnen Formeln gründlich getestet sind und funktionieren, setzt man sie zusammen. Dabei beginnt man von außen nach innen, bzw. bei der vorstehenden Formeln von unten nach oben. Um zu vermeiden, dass das Programm relative Adressen verbiegt, kopiert man nicht die Zelle, sondern die Zeichenfolge der Formel in der Formel-Eingabezeile.
- Markieren und kopieren Sie die Zeichenfolge der Formel =INDIREKT(B7) in der Eingabezeile der Zelle B8.
- Fügen Sie die Zeichenfolge in der Eingabezeile der Zelle B4 ein.
- Markieren und kopieren Sie die Zeichenfolge der Formel ADRESSE(22+B6;2;1) ohne Gleichheitszeichen in der Eingabezeile der Zelle B7.
- Setzen Sie die ADRESSE-Formel aus B7 in die INDIREKT-Formel anstelle des Bezuges B7 ein.
- Die zusammengesetzte Formel sieht jetzt so aus:
- Setzen Sie jetzt die VERGLEICH-Formel aus der Zelle B6 an die Stelle der Gesamt-Formel, wo B6 steht.
- Man setzt also eine verschachtelte Formel zusammen, indem man jeden Zellbezug durch die Formel ersetzt, die in der betreffenden Zelle steht. Wichtig ist, dass man das Gleichheitszeichnen nur bei der ersten Formel überträgt. Danach kann man das Verfahren formell weiter führen und macht mit etwas Übung keine Fehler mehr.
⇑ ↑ C.3 Tabellen erweitern ↓ ⇓
Die gelbe Tabelle enthält die Urwerte für das Diagramm
Das Diagramm im Bild stellt die Verteilung der Noten dar, die in der gelb unterlegten Tabelle eingetragen sind. Für die Notenverteilung einer anderen Klasse erstellt man das Diagramm natürlich nicht neu, sondern kopiert das ganze Tabellenblatt. Wenn die andere Klasse größer ist, muss die gelbe Tabelle vergrößert werden.
Die schlechte Methode zum Vergrößern der gelben Tabelle ist es, alle Formeln zu ändern, die sich auf die gelbe Tabelle beziehen. Im Beispiel müsste man dazu herausfinden, dass die gelben Urwerte erst im grünen Bereich klassiert werden müssen, bevor im Diagramm eine Verteilung dargestellt werden kann. Anschließend müsste man in funktionierende Formeln eingreifen, und davon ist immer abzuraten.
Die einfachere Methode zum Vergrößern der gelben Tabelle ist es, neue Zeilen bzw. Spalten in die Tabelle einzufügen. Beim Einfügen werden alle Formeln automatisch an die größere Tabelle angepasst, und man braucht den Aufbau der Formeln gar nicht zu kennen.
Im Beispiel fährt man über die Zeilennummern 14 bis 18 und wählt mit einem rechten Mausklick das Kontextmenu - Zellen einfügen, um 5 neue Zeilen einzufügen. Wichtig ist es, nicht die erste und letzte Zeile/Spalte zu markieren, weil es dann manchmal zu Problemen kommt.
Übrigens sind meine Tabellen meist farbig hinterlegt, damit ich ihre Grenzen leichter wieder finde. Die Farbe wird beim Zellen einfügen ebenfalls automatisch erweitert.
⇑ ↑ C.4 Formulare ↓ ⇓
Enges Zellenraster für komplizierte Formulare (ohne Gitterlinien)
Formulare enthalten Formularfelder, die oft unterstrichen oder umrahmt sind.
Wenn diese Formularfelder regelmäßig angeordnet sein sollen, kann man für jedes Formularfeld eine Zelle vorsehen. Die Größe der Formularfelder kann man dann mit der Größe der Zelle verändern .
Wenn man verschieden große Formularfelder in komplizierter Anordnung benötigt, ist dieses Verfahren nicht sinnvoll, weil die Breite übereinander liegender Formularfelder nicht unabhängig voneinander verstellt werden kann.
In diesem Fall ist es sinnvoll, mit einem engmaschigen Raster zu beginnen und dieses Raster nicht mehr zu verändern. Die Formularfelder erzeugt man dann durch Zusammenfassen von Zellen .
Wenn man wie im Bild die Gitterlinien nicht benötigt, ist es noch nicht mal nötig, die Zellen zusammenzufassen. Es genügt, die gewünschten Zellen zu markieren und dann mit Linien und Rahmen zu versehen.
Geplante Erweiterungen
- Kopiertechniken
- Zahlenreihen
- rel. / abs. Adressierung
- SUMME(..) statt I1 + I2 +…
- leichter zu lesen, weniger Fehler
- erweiterbar: Zeilen und Spalten einfügen
- Geschicktes Anordnen in Tabellen
- Dokumentation
- Mit leicht überprüfbaren Zahlen testen
- Summen nach oben
- Formatieren so spät wie möglich
- Kommentieren Sie ein Tabellenblatt immer so, dass es auch eine andere Person oder Sie selbst in 2 Jahren verstehen.
- Markieren Sie Eingabefelder, damit man sie schnell findet.
- Sperren Sie Berechnungsfelder, in denen nichts eingegeben werden muss.
⇑ ↑ Anhang D: numerische Fehler der Programme ↓ ⇓
⇑ ↑ D1: =Ganzzahl() ↓ ⇓
Die Funktion =Ganzzahl() schneidet von einer Zahl die Kommastellen ab, =Ganzzahl(2,7) ergibt 2.
Probleme können auftreten, wenn eine vorhergehenden Rechnung intern ein Ergebnis wie 1,9999999999999999999 ergeben hat. Nach außen tritt die Abweichung nicht auf, weil diese Zahl als 2 dargestellt wird. Auch bei weiteren Berechnungen mit dieser Zahl tritt kein Problem auf, weil die Abweichung sehr klein ist bzw. durch interne Rundungsalgorithmen korrigiert wird.
Nur bei =Ganzzahl(1,9999999999999999999) kann aus einer 2 plötzlich eine 1 werden und damit das Ergebnis deutlich verfälschen.
Lösen kann man dies Problem, indem man zum Argument innerhalb =Ganzzahl() einen sehr kleinen Wert addiert. Zum Beispiel ergibt =Ganzzahl(1,9999999999999999999+0,000001) das richtige Ergebnis 2.
Ein Beispiel für diesen Fehler, der bei MS Excel97 und OpenOffice1.0 bzw. StarOffice6.0 auftritt, finden Sie in der Übung Sammelbestellung .
⇑ ↑ D2: =BinomVert() ↓ ⇓
In MS Excel 97 rechnet die Funktion für die untere Summenwahrscheinlichkeit der Binomialverteilung nicht korrekt. Beim Ereignisanteil p=0 wird in einigen Fällen die untere Summenwahrscheinlichkeit 0 statt 1 berechnet. Zum Beispiel gibt die Funktion =BINOMVERT(2;32;0;1) das Ergebnis 0 statt 1. Man kann das Problem lösen, indem man mit p=0,000001 rechnet.
Beispiel: Binomiale_Verteilung.XLS . OpenOffice / StarOffice machen diesen Fehler nicht.
⇑ ↑ D3: =HypgeomVert() ↓ ⇓
OpenOffice1.0 bzw. StarOffice6.0 berechnet die Formel =HypgeomVert(1;4;152;10000) nicht korrekt. Die Formel rechnet erst dann korrekt, wenn man den Wert 152 auf mindestens 142 verkleinert.
Beispiel: hypergeometrische_Verteilung.ods . MS-Excel macht diesen Fehler nicht.
⇑ ↑ Anhang E verwendete Begriffe ↓ ⇓
absolute Adresse ; bedingte Formate ; Formatieren ; Formatvorlage ; Funktionsleiste ; harte Formatierung ; Hochkomma ; kaufmännisches Und; Kontextmenü; Menüleiste, Rechenleiste ; relative Adresse ; RMK ; Spaltenköpfe; Statusleiste ; String ; Symbolleiste ; Tabelle ; Variable ; weiche Formatierung ; Zahlenformat ; Zeichenkette ; Zeilenköpfe; Zelle ;
⇑ ↑ Anhang F - Funktionen ↓ ⇓
⇑ ↑ F.1 Statistik ↓ ⇓
Normalverteilung
Mittelwert und Standardabweichung
Mittelwert und Standardabweichung sind die Parameter einer Normalverteilten Messreihe. Wenn sie bekannt sind, kann man viele Beurteilungen und Auswertungen vornehmen, ohne jedesmal mit unter Umständen tausenden von Messwerten rechnen zu müssen.
In der Praxis sind Messreihen aber selten genau Normalverteilt, deshalb kann man auf die Urwerte nicht ganz verzichten.
- =Mittelwert(Werteliste)
berechnet den Mittelwert einer Liste - =STDABW(Werteliste)
berechnet die Standardabweichung einer Liste mit dem in Europa üblichen Teiler n-1 - =STDABWN(Werteliste)
berechnet die Standardabweichung einer Liste mit dem Teiler n
Summenhäufigkeit
Summenhäufigkeiten beantworten zB. die Fragen, wie viele Prozent einer Normalverteilten Produktion, von der Mittelwert und Standardabweichung bekannt sind, unterhalb, oberhalb oder zwischen zwei Grenzwerten liegen.
- =NORMVERT(Grenzwert; Mittelwert; Standardabweichung; WAHR)
untere Summenhäufigkeit berechnet, welcher Anteil einer Normalverteilten Reihe einen kleineren Wert als der Grenzwert hat. Damit kann ermittelt werden, wie groß der Anteil einer Normalverteilten Fertigung unterhalb des unteren (Toleranz-)Grenzwertes ist. - =1-NORMVERT(Grenzwert; Mittelwert; Standardabweichung; WAHR)
obere Summenhäufigkeit berechnet, welcher Anteil einer Normalverteilten Reihe einen größeren Wert als der Grenzwert hat. Damit kann ermittelt werden, wie groß der Anteil einer Normalverteilten Fertigung oberhalb des oberen (Toleranz-)Grenzwertes ist. - =NORMVERT(oberer Grenzwert; Mittelwert; Standardabweichung; WAHR) -
NORMVERT(oberer Grenzwert; Mittelwert; Standardabweichung; WAHR)
berechnet, welcher Anteil einer Normalverteilten Reihe zwischen den Grenzwerten liegt. Damit kann ermittelt werden, wie groß der Anteil einer Normalverteilten Fertigung innerhalb der (Toleranz-)Grenzwerte liegt.
Umkehrfunktion der Summenhäufigkeit
Die Umkehrfunktion der Summenhäufigkeit beantwortet zB. die Fragen, wo eine Grenze liegen muss, damit 90% der Fertigung darunter liegt.
- =NORMINV(Unterschreitungsanteil; Mittelwert; Standardabweichung)
berechnet die Grenze so, dass gerade der Unterschreitungsanteil, zB. in Prozent, darunter liegt.
Beispiel: In der Fertigungstechnik mit statistischer Prozessregelung benötigt man die Grenzen, innerhalb derer 95% (99%) der Fertigung liegen. Da die Normalverteilung symmetrisch ist, heißt das, dass 2,5% (0,5%) unterhalb des unteren Grenzwertes liegen. 2,5% (0,5%) werden deshalb als Unterschreitungsanteil eingesetzt. - =NORMINV(1-Überschreitungsanteil; Mittelwert; Standardabweichung)
berechnet die Grenze so, dass gerade der Überschreitungsanteil darüber liegt.
⇑ ↑ Anhang G weitere_Uebungen ↓ ⇓
⇑ ↑ G.1 Datenbankfunktionen ↓ ⇓
Aufgabe:
Gegeben: Liste für Einfach-Stichprobenpläne nach AQL. Es handelt sich um eine Liste der Art
Bei Liefermengen von 26 bis 50 Stück entnimmt man eine Stichprobe von 5 Stück
Bei Liefermengen von 51 bis 90 Stück entnimmt man eine Stichprobe von 20 Stück.
Eingabe: Liefermenge, z.B. 55
Ausgabe: Stichprobenumfang
Funktionen: =DBAuszug()
Lösungen mit Anleitung: PDF, LibreOffice, Excel97
⇑ ↑ G.2 Kalender ↓ ⇓
Themen: Datumsformate, stark verschachtelte Funktionen, bedingte Formate, Datenbankfunktionen
Anleitung: PDF
Musterlösung: ODS | PDF
⇑ ↑ G.3 Spiele ↓ ⇓
Themen: in Tabellenfunktionen eingebaute Spiele
Funktionen: versteckte Funktionen
Anleitung: PDF
Links für versteckte Spiele, für
- Easter Eggs (05/2009)
- The Easter Egg Archieve (05/2009)
⇑ ↑ G.4 Weitere Blätter ohne große Erklärungen ↓ ⇓
- Spannungs-Dehnungs-Diagramme: Mal eben Wertepaare für eine Aufgabe zum Zugversuch finden? Diese Blatt schätzt Spannungs-Dehnungs-Wertepaare aus den Festigkeitswerten (E, Rp0,2, Re, Rm, A) eines Werkstoffes ab und stellt sie als Diagramm dar. Es sind Werkstoffe mit und ohne ausgeprägter Streckgrenze möglich. Die Spannungs-Dehnungs-Wertepaare werden mit den Angaben für die Zugprobe auch in Kraft-Verlängerungs-Wertepaare umgerechnet und dargestellt. In einem weiteren Blatt können gegebene Wertepaare auch ineinander umgerechnet werden.
Formate: LibreOffice, MS-Excel97 .
⇑ ↑ Links ↓ ⇓
⇑ ↑ Kurse und Lösungen ↓ ⇓
- Link: Ein umfangreiches Skript mit dem Thema "Grundzüge der Datenauswertung mit Excel und OpenOffice" finden Sie auf der Seite von Jan Schmidt mit DeTe . (06/2009)
- Link zu Dr. Bommhardt: Arbeitsblätter zu MS Excel und anderen Programmen, bevorzugt aus dem Nahrungsbereich. (10/2007)
- Netschool.at von Renate + Ernst Frey: Kurse zu StarOffice und MS-Office (Textverarbeitung und Tabellenkalkulation). (10/2003)
- Dieter Heidorn: Einführungskurs und Übungsbeispielen zu StarCalc. (10/2003)
- Helmut Kohorst: Excel-Lösungen zur Stochastik und zur grafischen Darstellung von Funktionen. (04/2006)
- Link: OpenOffice.de: Hier kann man OpenOffice kostenlos herunter laden und erhält Hilfe. (02/2005)
- Link: Werner Roth bietet umfassende Informationen zu StarOffice. (04/2002)
⇑ ↑ Sonstiges ↓ ⇓
- Der Artikel Tabellenkalkulation im Wiki der Zentrale für Unterrichtsmedien im Unterricht e.V. (ZUM) enthält Links für Lehrer. (04/2006)
- OpenOffice: Hier kann man OpenOffice kostenlos und legal herunterladen und dann alle Übungen nachvollziehen. (02/2005)